新しいツールを使い、古い問題を解決する

アンドリュー・ロブ准教授、新型コロナによるロックダウンの期間、「丸い穴の中に四角い杭は入るのか？」という1世紀にわたる問題を解決

アンドリュー・ロブ准教授は、2019年10月、客員数学教授プログラムに参加するため、沖縄科学技術大学院大学（OIST）にやって来ました。このプログラムは、有望な数学者を半年間OISTに招聘し、シンポジウムの開催や研究への貢献を目的としています。ただしこの時、ロブ准教授は、世界的な新型コロナパンデミックの影響で、本島での滞在期間が数ヶ月延長されるとは知らずにいました。

それでも、日本の亜熱帯地帯で封鎖期間中に過ごした数ヶ月間は、ロブ准教授にとっては無駄になりませんでした。ボストン大学のジョシュア・グリーン教授との共同研究を通じ、ロブ准教授は100年以上も未解決のままだった数学的問題、「どんなに滑らかなループに対しても、その中に収まる長方形は存在するか？」に着目しました。

アンドリュー・ロブ准教授は、ダラム大学准教授。2019年10月から2020年8月までOISTの客員数学教授プログラムに参加。

オックスフォード大学で数学の修士号を取得し、ハーバード大学で博士号を取得したロブ准教授は、3次元および4次元空間のトポロジーと幾何学を専門としています。

「幾何学は何世紀にもわたり、数学分野において最も重要な分野でした。そして幾何学から距離や角度に関する情報を取り除けば、トポロジーの分野ができあがります。トポロジーの空間は、現代における数学の多くの礎となっているのです。つまり多くの数学における分野は、各分野に関連する他の構造と重なるトポロジー空間について研究している、と考えることができるのです」と、ロブ准教授は説明します。

丸い穴に四角の杭を打つ

「丸い穴に四角い杭を打つ」という概念は、格言に似ているので馴染みがあるかもしれません。この格言は、特に適していない環境に適合しようとする個人を指したものです。しかし数学的には、この格言は異なる意味を持っています。「四角い杭」に関する疑問は、ドイツの数学者オットー・テプリッツが1911年に初めて投げかけたものでした。テプリッツは、すべてのジョルダン曲線、すなわち閉じた重なりのない曲線には、四角が含まれていると定理化しました。この問題は今も未解決のままですが、ロブ准教授とグリーン教授は、類似した「長方形の杭の問題」に取り組み、ロブ准教授はその後、OISTの学長主催講演会で、この研究についての議論を投げかけました。

ロブ准教授は、四角い杭製造工場を受け継いだばかりの人についてのストーリーから講義を始めました。「杭はすべて四角です。もし誰かが四角い穴を持ってきたら、その穴の中に収まる四角い杭を作ることができるでしょう。でも誰かが円形の穴を持ってきたとしても、円周上の４つのポイントを見つけるだけで、その穴に合う四角いくいを作ることはできます。」とロブ准教授は説明します。

しかし、この四角い杭の問題はさらにこの理論を発展させます。円や四角い穴だけを見るのではなく，あらゆるジョルダン曲線を見るのです。理論的にはループ内に収まる四角形が常に存在し、その四隅が曲線の端に接触しています。

「この問題は説明するのは簡単ですが、数学的な仕掛けを作るのが非常に難しいので、興味深い問題なのです」とロブ准教授は話します。

アンドリュー・ロブ准教授が、学長主催講演会のプロモーションビデオで、長方形の杭の問題の背景を説明。以下にレクチャーの全記録あり。

1970年代、長方形の杭の問題への解への前進がありました。数学者ハーバート・ヴォーンが、長方形を4つの点の集合として考えることを止め、代わりに2つの点のペアの関係として考えるようにしたのです。このように考えると、各長方形には中点、つまり4つの点が出会う場所があります。ループになると、その点は曲線上の2つの点のちょうど真ん中にあたります。ハーバート・ヴォーンは、ループに着目し、すべてのペアとなっている点間のすべての中間点を定め、平面上にプロットしてみました。すると、見たこともないものができることを発見しました。

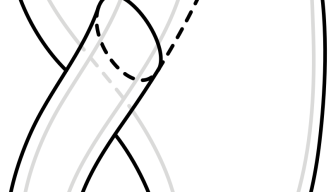
このようにして、「メビウス・ストリップ」と呼ばれるねじれた閉じたループが誕生し、研究者たちに新しい遊び道具を提供してくれたのです。いまや数学者は、数十年前からあるこの問題を解くためにメビウス・ストリップを使っていますが、ロブ准教授とグリーン教授が完成させた研究の特徴は、現代のフレームワークであるシンプレクティック幾何学を使うことができたという点です。 Quanta Magazine 誌に掲載された最近の記事の中で，ライターのケヴィン・ハートネット氏がこの問題の歴史を掘り下げ，2 人の数学者による業績が今までの数学者とはいかに異なるかを正確に説明しました。

2本のメビウス・ストリップが一緒になると、クラインの壺という珍しい瓶のような物体を形成し、中で交差する。

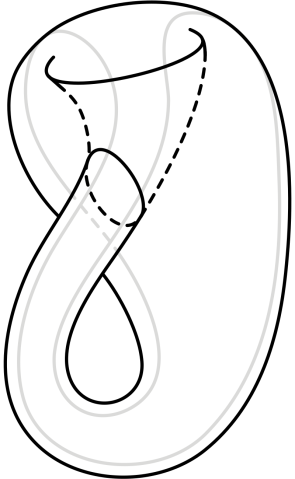
二人の数学者は今回、このメビウス・ストリップを別の幾何学的空間に抜本的に移行させました。二次元空間から四次元空間へ、シンプレクティックな四次元空間へと移行させたのです。

ふたつのメビウス・ストリップがひとつになると，3次元空間では中で交差するクラインの壺を形成します。しかし４次元空間では，クラインの壺には十分なゆとりが与えられているので，中で交差する必要はありません。しかし、シンプレクティックな４次元空間では、クラインの壺は中で交差しなければならないという条件が再び出てくるのです。この交差点は，ロブ准教授とグリーン教授が長方形のくいの問題を解く際の鍵となりました。

二人の数学者は、この現代的な枠組みを使うことで、一世紀以上もの間解けなかった問題を解くことができたのです。「古い問題に現代の技術をどのように適用できるかを考えるべきです。」と、ロブ准教授は、未解決の理論や問題に立ち返ることを数学者に勧めたいと語っています。