数学には、非常に正確に宇宙を説明する力があるため、現代の物理学者たちは実在性そのものが数学からなることを示してきました。こういうと、高校時代の代数を思い出して、「悪夢のようだ」と戸惑われる方もいらっしゃるでしょうが、OISTの数理理論物理学ユニットの氷上忍教授にとっては、定理からなる宇宙は喜びに満ちた夢を生み出すものでもあります。「ただの夢にすぎませんが」と氷上教授は続けます。
「数学的証明の単純性は非常に美しいものです。自分の研究結果が妥当であるか否かを知る手段でもあります。証明が美しくなければ、何かが間違っていることになります。ただし、方程式の魅力に取りつかれると、数学が実際にできることを重要視しすぎることにもなります。」
数学と理論物理学の世界で40年以上教鞭をとってきた氷上教授は、数によって説明可能な現象を非常に多く目にしてきました。その中にあっても、数学ではつかみきれないものも、また逆に私たちや、私たちの生きる宇宙とは関係のない数学的な考えもあると述べています。
高校時代、同級生たちが日常生活と微積分にどんな関係があるのかと考えている間に、氷上少年は数字が持つ力に魅了され、時間を見つけてはあらゆる高度な数学分野を勉強するようになりました。「高校時代の数学の先生から刺激を受け、数学にすっかりはまってしまいました」と氷上教授は述べます。「しかし、同時に、数字と方程式だけでは満足しなくなりました。それをどのように応用したらよいのかを知りたくなったのです。」その後、東京大学で物理学を専攻し、大小問わず万物における相互作用の説明に、いかに数学を用いるかを学ぶと、氷上教授はそこに天職を見出したことに気付きました。
この20年間氷上教授は自身の研究生活を、膨大な収集データの中に潜む相関性を見出す数学的手法であるランダム行列理論に捧げてきました。ランダム行列理論は、ありふれた組み合わせツールではありません。この数学的手法は、膨大な乱数について、その組み合わせが個々の数字の増減によって経時的に変化しても、その中から相関性のあるデータ群を見出すことに用いられます。
20世紀半ば、ノーベル賞受賞者であるユージン・ウィグナー博士らは、原子核物理学の謎を解明するランダム行列理論を初めて構築しました。「東京で学生だった頃、ランダム行列理論はあまり注目されておらず、関心を寄せていたのは物理学者だけでした」と氷上教授はふりかえります。しかし、ランダム行列理論は、理論物理学における重要性を維持しながら、現在では経済学から生物学まで幅広い分野で応用されるまでになりました。
ランダム行列理論を、経済学者は株の上下に相関性を見出すために用い、生物学者は各種タンパク質の細胞又は組織内における発現レベルの相関性を見出すことに関心を寄せるかも知れません。いずれの場合も、ランダム行列理論は、自動車会社と自動車部品製造会社の株のように、既に関連性がわかっている実体間の相関性の確認や、予測できない新たな相関性の発見に用いられます。ランダム行列理論は相関性の検出に有用ですが、ある特定の現象が相関性を失うことによってランダムに生じるか否かを研究者に教えもしてくれます。
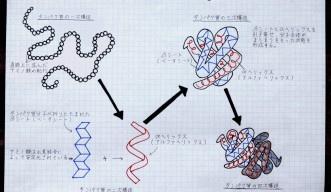
人類、とりわけ研究者たちが、自分を取り囲む世界について計測するようになってからというもの、氷上教授および同教授と同分野の他の研究者らは、関心のある相関性について調べることのできるデータを豊富に得ています。氷上教授が初めてランダム行列理論に取り組み始めた頃、弦理論において、さまざまな弦における振動の相関性を明らかにする手法を採用しました。弦理論とは、電子または光子などの素粒子は粒子などではなく、振動する弦であり、弦の振動によって電荷と質量が与えられるとする素粒子物理学の研究領域です。OISTの学際的環境の中で研究を続けるうちに、氷上教授は複雑な生物系、とりわけ、最終的には生体組織の構成要素となる立体的なタンパク質を構築するための重要なプロセス、すなわちアミノ酸の複雑な折り畳みと絡み合いにおける相関性の解明に、ランダム行列理論を利用することに特別な関心を持つようになりました。
氷上教授は語ります。「確固とした数学的定理が理論を導き、それから実験によって立証されることがあります。しかし、実験的証拠が理論を変えるほどの影響を有し、その後数学が実証することもあるのです。いずれにしても、生物学と同様に物理学においても、知識を構築するためには、実験、数学および理論が同時に働く必要があります。そしてOISTには、的確にその作業をこなす実験主義者、数学者および理論家が揃っています。」
