原点回帰
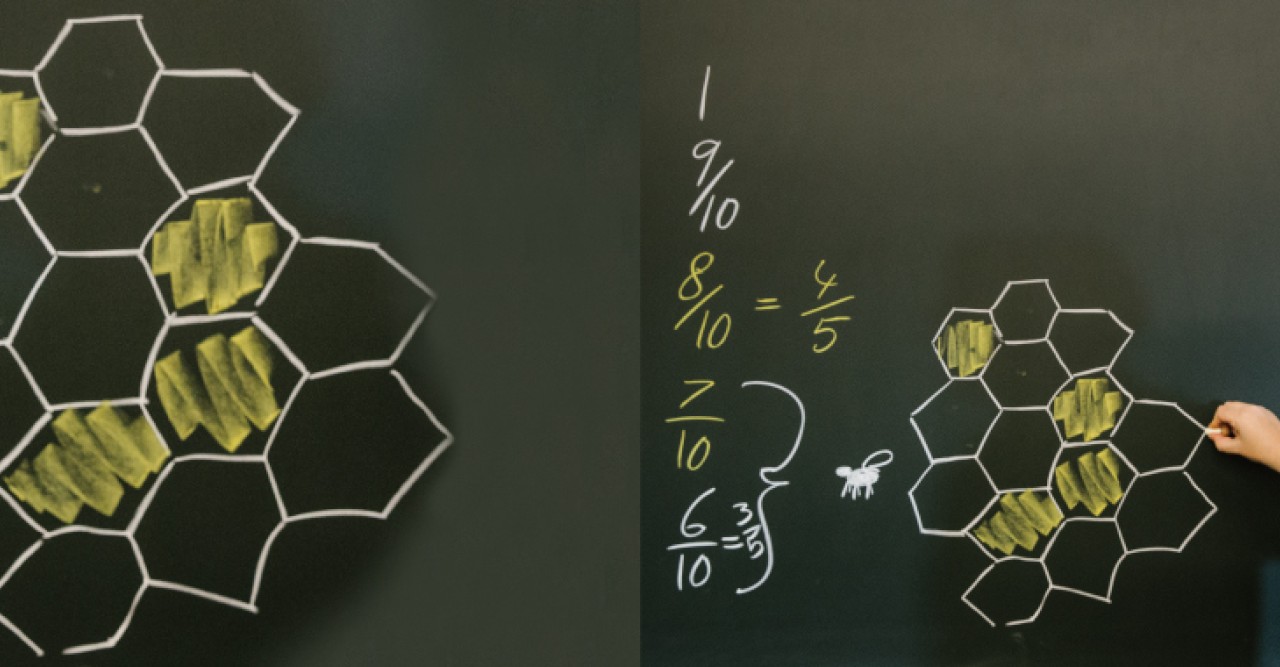
Frontiers in Computational Neuroscience 誌に掲載された沖縄科学技術大学院大学のロバート·シンクレア准教授の論文は、現代科学においても、有理数や単純な比率を用いて実験結果を読み解く余地が残されていることを示しています。スーパーコンピュータが主に科学的分析を行う現代において、古くからの基本的なアプローチに十分な関心が向けられていないと同准教授は指摘します。しかしこの基本的なアプローチこそが、非常に複雑なテーマやシステムを単純化し、自然界に対する私たちの理解を大いに啓発してきたのです。メンデル(1822~1884)はまさにこのアプローチをとり植物の遺伝に関して単純に数や比率を調べることで、遺伝学における最も重要な法則のいくつかを発見、記述してみせました。数学と他の様々な科学分野を結びつけることは現代科学においても意義があり、有理数のような単純なものにも果たす役割があり得ると同准教授は考えています。
様々な細胞種から構成されている組織は、DNA上にプログラムされた情報に基づいて秩序的、決定論的な発生過程から生み出されたものか、もしくは環境に応じて、あるいは状況に応じて予測が立てにくい無秩序的、確率論(偶発)的な発生過程から生じたものかに分かれます。ここで重要なのは、その両方のシステムが共存し、機能していると仮定できるということです。少なくとも自然界には偶発性の方を優先的に選ぶ何らかの選択圧が存在し、あえて決定論的に扱わないことで、不必要に複雑化したり非効率化したりするのを防いでいるようなのです。シンクレア准教授は組織の成長において、これらいずれのタイプもすべてに該当するとは限らないことに早くから目を付けました。実際には、状況に応じて、どのタイプが適切なのか明白に使い分けられていることがあるのです。
シンクレア准教授は、この2つの方法のいずれかを用いてレゴを組み立てることを例に説明を続けました。「レゴの城を組み立てる際、説明書を参照する人もいるでしょう。または、レゴの箱にある城の見本写真を見て、その写真のようになるまで色々な形を試してみる人もいるでしょう。ここで興味深いのは、説明書に従うよりもただ写真を見て作る方が好まれるのはどのような場合かということです。どちらの方法をとっても結果として出来上がるのはレゴの城です。しかしそこに行き着くまでのプロセスは、何を得ようとしているか、つまりどのような城を作ろうとしているかによって異なる場合があるのです。」
少数の細胞種で構成された集団を単純に繰り返して組織を形成する場合、細胞種間での調整がしやすく、最終的な組織の細胞種の比率も単純なものに落ち着きます。その例として、シンクレア准教授は細胞種の比率が1:3の場合を挙げます。このような系の場合、細胞が4つあれば基本単位が完成し、それを何度も複製していけば、細胞種の比が1:3の組織を形成できます。このようなプロセスは決定論的であると言えます。一方、目標とする細胞種の比率が複雑になれば、分数の分母が大きくなるため決定論的システムで達成することが難しくなってきます。この時、代替手段としてうってつけなのが偶発性です。その一例として挙げられのが、異なる細胞種が10:33の比率で混在する組織です。この比率を達成するのは容易ではありません。なぜなら基本単位をつくるために必要な細胞の総数はこの場合43にもなり、わずか4つでは済まされないからです。
このような大規模で複雑な系に決定論的なアプローチを適用しようとすれば、細胞システムの成長を制御する発生プログラムの側からすると難しすぎて手に負えなくなる可能性があります。比率がますます複雑になったり、分子の分母がさらに大きくなったりする状況では、むしろ基本単位を設けず確率論的手段をとり入れ偶然に任せる方が、細胞の混合組織を得やすいかもしれません。
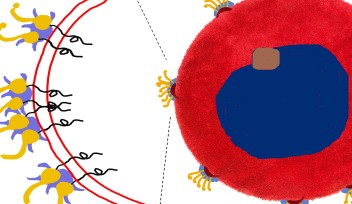
現実世界では、決定論的メカニズムと確率論的メカニズムの両方が使われています。その一例をショウジョウバエの複眼の構造に見ることができます。ここでは、0から1の間の有理数を用いて、シンクレア准教授の仮説に出てくる確定性(決定論)と偶発性(確率論)について考えていきます。そうすると、眼の2つの部分について、ある部分は確定性への傾向を示し、もう一方は偶発性への傾向を示す理由が説明できるのです。まず、複眼の構成単位である個眼の各々が持つ光受容細胞の数は常に8個と決まっています。眼構造のこの点に関しては決定論的な発生が関与していると考えられ、実際に成長過程の観察からもそのように見えます。一方、個眼の持つ感光色素の場合はもっと複雑です。 8種類ある細胞のうちの1つでは、2種類ある色素のどれか1つが発現します。この2種類の色素のうち、ある特定の色素が発現している比率は60~70%です。これは、眼の構成細胞に見られる他の測定可能な比率に比べると、最小公分母が大きいため単純な有理数では表しにくい範囲です。そのため、色素の選択に関しては確率論的システムを介した方が実行しやすく、実際にそうであることがわかっています。
このような研究を通じ、シンクレア准教授は、単純な方法を用いて複雑なシステムをとらえようとする古典的な科学的思考法が、今日の科学においても有効なものであるという考え方にもっと目が向けられたらと考えています。同准教授の願いは、確定性か偶発性かの傾向を明確に示すこのシンプルなアプローチが、今後発生生物学の分野で研究者が実験を組み立てる際にヒントを与えるものとなってほしいということです。つまり、それが理論の要点であり意義なのです。
(ショーン トゥ)