By Ivan SHPUROV
The world around us is full of complex evolving structures. From a certain point of view, patterns of gene regulation within every living cell, networks of neurons in the brains, and complex social webs of interaction humans weave both online and offline, can be seen as a similar entity – self-optimizing structures capable of learning, evolving and adapting to new challenges and environments. We believe, that by applying mathematical framework developed by neural network practitioners and theorists in the science of complexity, we could achieve better understanding of many phenomena occurring both in the natural world and in the realm of artificial life.
Thus, by modeling genes as nodes of neural graphs, connected by vertices of correlated expression, we could hypothesize how evolution could “remember” previously achieved optima on the adaptive landscape as attractors of this genetic network and then recall them when organism encounter similar environment. This unorthodox approach could help widen our understanding of numerous evolutionary phenomena, such as convergent evolution of unrelated species or punctuated equilibria.
At the same time, when we allow individual neurons of the network to behave like selfish agents pursuing their individual gain thought the evolution out of their interactions, governed by a few simple rules, would emerge a structure capable of self-organizing using Hebbian learning and displaying complex behavior.
Case study 1 - Watsons network
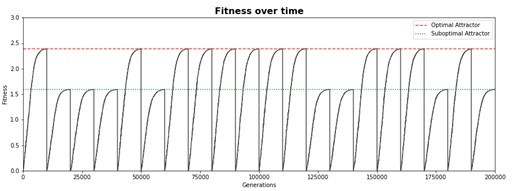
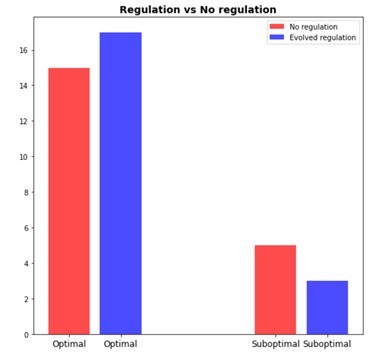
Watson and Wagner proposed a simple computational model of genetic network, which, however, is capable of demonstrating interesting behavior. Gene expression is modeled as a numeric vector while epistatic interactions between genes are represented by a 2D matrix. During the simulated evolution studies both acquire random mutations.
Case study 2 - Yeast model
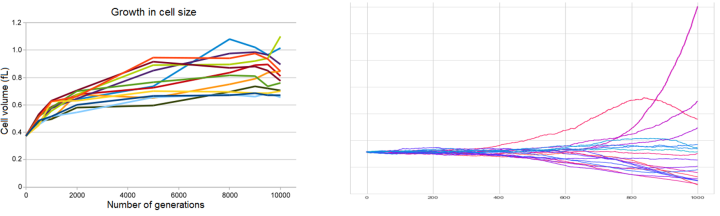
Evolution theory is indeed the cornerstone of modern biology, yet it is almost as difficult to model it in controlled lab conditions as it is important. Two famous experiments dedicated to artificial evolution in lab environments are the E. coli long term evolution study (Barrick et al., 2009) and Yeast experiment (Kryazhimskiy, Rice, Jerison, & Desai, 2014). Both experiments confirmed existing theories but also led to a rise of new questions. These projects attempt to create robust computational model of evolving population to interrogate how regulatory interactions could be responsible for evolutionary patterns observed in the laboratory conditions.