FY2021 Annual Report

Quantum Systems Unit

Professor Thomas Busch

Abstract

With the passing of another five-year review last year, and the borders of Japan opening again, the group is expanding and moving into new areas and topics. Broadly speaking we are now working on five different strands of ideas: strongly correlated systems, superfluid systems, many-body tological system, quantum thermodynamics and near-field optics using nanofibers.

1. Staff

• Dr. Pham Le Kien, Staff Scientist
• Dr. Thomás Fogarty, Staff Scientist
• Dr. Karol Gietka, JSPS Fellow/Postdoctoral Scholar
• Dr. Juan Polo Gomez, Postdoctoral Scholar
• Dr. Hao Lyu, Postdoctoral Scholar
• Dr. Sayyare Aksu, Postdoctoral Scholar
• Dr. Kritika Jain, Postdoctoral Scholar
• Ms. Ayaka Usui, PhD Student/Junior Research Fellow
• Mr. Christopher Campbell, PhD Student
• Mr. Tim Keller, PhD Student
• Ms. Friederike Metz, PhD Student
• Mr. Lewis Ruks, PhD Student
• Mr. Muhammad Sirajul Hasan, PhD Student
• Mr. Mohamed Boubakour, PhD Student
• Mr. Yuta Itoh, PhD Student
• Mr. Jose Carlos Pelayo, PhD Student
• Ms. Keerthy Menon, PhD Student
• Mr. Tai Tran, PhD Student
• Mr. Hoshu Hiyane, PhD Student
• Ms. Sarika Sasidharan Nair, PhD Student
• Ms. Sawako Koki, Research Unit Administrator

Rotation Students

• Mr. Morihiro Ohta (May-August, 2021)
• Ms. Sarika Sasidharan Nair (May-August, 2021)
• Mr. Fabian Hillebrand (September-December, 2021) *worked remotely
• Ms. Pramitha Praveen Kamath (September-December, 2021)*worked remotely
• Mr. Raul Alejandro Hidalgo Sacoto (January-April, 2022)*worked remotely

Research Interns

Ms. Bandita Das, University of Hyderabad, India (July 01, 2021 - December 24, 2021) *VRS, worked remotely
*two internships was cancelled due to COVID-19 restriction

2. Collaborations

2.1 Quantum Thermodynamics

• Type of collaboration: Joint research
• Researchers:
  • Prof. S. Campbell, University College Dublin, Ireland
  • Prof. J. Goold. Trinity College Dublin, Ireland

2.2 Shortcuts to adiabaticity

• Type of collaboration: Joint research
• Researchers:
  • Dr. A. Ruschhaupt, University College Cork, Ireland
  • Prof. Xi Chen, Shanghai University, China and University of Bilbao, Spain

2.3 Cold atoms and optical nanofibers

• Type of collaboration: Joint research
• Researchers:
  • Prof. Sile Nic Chormaic, OIST Graduate University, Japan

2.4 Quantum Thermal Engines

• Type of collaboration: Joint research
• Researchers:
  • Prof. Artur Widera, Kaiserlautern University, Germany
  • Prof. Erik Lutz, Stuttgart University, Germany

2.5 Nonlinear Condensate Dynamics

• Type of collaboration: Joint research
• Researchers:
  • Prof. Yongping Zhang, Shanghai University, China

3. Activities and Findings

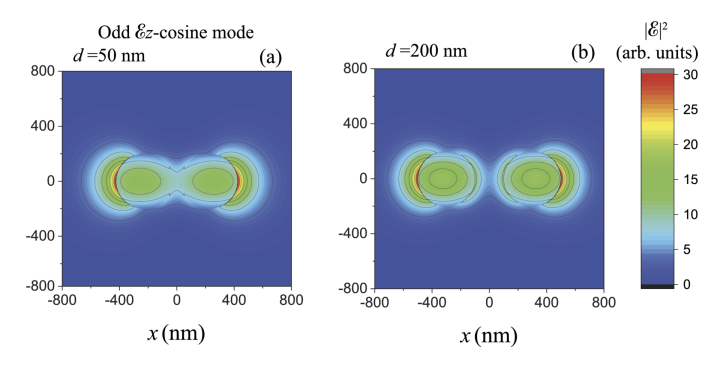
3.1 Spatial distributions of the fields in guided normal modes of two coupled parallel optical nanofibers

We have studied the cross-sectional profiles and spatial distributions of the fields in guided normal modes of two coupled parallel optical nanofibers and shown that the distributions of the components of the field in a guided normal mode of two identical nanofibers are either symmetric or antisymmetric with respect to the radial principal axis and the tangential principal axis in the cross-sectional plane of the fibers. The symmetry of the magnetic field components with respect to the principal axes is opposite to that of the electric field components. We show that in the case of odd E_z-sine modes, the electric intensity distribution at the two-fiber center attains a local minimum of exactly zero, which can be used as a trapping potential.. We also find that the differences between the results of the coupled mode theory and the exact mode theory are large when the separation distance between the fibers is small and either the fiber radius is small or the wavelength of light is large. 

Figure: Cross-sectional profile of the electric intensity distribution of the field in the odd Ez-cosine mode of two identical parallel nanofibers. Publication:
Spatial distributions of the fields in guided normal modes of two coupled parallel optical nanofibers
Fam Le Kien, Lewis Ruks, Sile Nic Chormaic, Thomas Busch
New J. Phys. 23 043006 (2021).

3.2 Cavity-enhanced magnetometer with a spinor Bose–Einstein condensate

We have proposed a novel type of composite light–matter magnetometer based on a transversely driven multi-component Bose–Einstein condensate coupled to two distinct electromagnetic modes of a linear cavity. Above the critical pump strength, the change of the population imbalance of the condensate caused by an external magnetic field entails the change of relative photon number of the two cavity modes. Monitoring the cavity output fields thus allows for nondestructive measurement of the magnetic field in real time and we have shown that the sensitivity of the proposed magnetometer exhibits Heisenberg-like scaling with respect to the atom number.

Figure: Schematic of the magnetometer. The atoms are strongly confined along the axis of an optical cavity and driven by two off-resonant transverse lasers with Rabi frequencies Ωj inducing internal atomic transitions |gj〉 ↔|ej〉. These transitions are also strongly coupled to two distinct standing-wave cavity modes aj with coupling strength Gj. The atoms can experience a Zeeman shift due to a static magnetic field B|| and/or a time-dependent magnetic field B⊥ cos(ωt), with the latter inducing transitions |g1〉 ↔ |g2〉. Publication:
Cavity-enhanced magnetometer with a spinor Bose–Einstein condensate
K. Gietka, F. Mivehvar, and Th. Busch
New J. Phys. 23 043020 (2021)

3.3 Cavity magnomechanical storage and retrieval of quantum states

We have shown how a quantum state in a microwave cavity mode can be transferred to and stored in a phononic mode via an intermediate magnon mode in a magnomechanical system. For this we have considered a ferrimagnetic yttrium iron garnet (YIG) sphere inserted in a microwave cavity, where the microwave and magnon modes are coupled via a magnetic-dipole interaction and the magnon and phonon modes in the YIG sphere are coupled via magnetostrictive forces. By modulating the cavity and magnon detunings and the driving of the magnon mode in time, a stimulated Raman adiabatic passage-like coherent transfer becomes possible between the cavity mode and the phonon mode. The phononic mode can be used to store the photonic quantum state for long periods as it possesses lower damping than the photonic and magnon modes. Thus our proposed scheme offers a possibility of using magnomechanical systems as quantum memory for photonic quantum information.

Figure: Input (left) and output (right) Wigner functions for the cavity mode with input cat state after storage for about 0.1ms. Publication:
Cavity magnomechanical storage and retrieval of quantum states
B. Sarma, Th. Busch, and J. Twamley
New J. Phys. 23, 043041 (2021).

3.4 Simulating the same physics with two distinct Hamiltonians

We have developed a framework and given an example for situations where two distinct Hamiltonians living in the same Hilbert space can be used to simulate the same physics. As an example of an analog simulation, we have discussed how one can simulate an infinite-range-interaction one-axis twisting Hamiltonian using a short-range nearest-neighbor-interaction Heisenberg XXX model with a staggered field. Based on this, we have shown how one can build an alternative version of a digital quantum simulator. As a by-product, a method for creating many-body maximally entangled states using only short-range nearest-neighbor interactions was found.

Figure: The set of all initial quantum states is given by S. Even if a quantum simulator Hamiltonian HQS is not the same as the target Hamiltonian HT, there still exists some set of states SQ that can simulate the physics of HT. If the overlap SS between the set of experimentally accessible states SA and SQ is not zero, the concept of using the connector can be used in analog quantum simulators. Publication:
Simulating the same physics with two distinct Hamiltonians
Karol Gietka, Ayaka Usui, Jianqiao Deng, Thomas Busch
Phys. Rev. Lett. 126, 160402 (2021) Editors' Suggestion

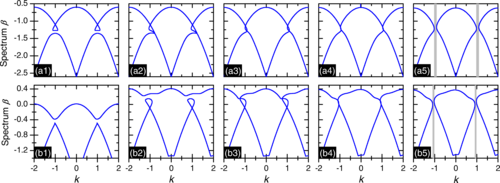
3.5 Asymmetric Loop Spectra and Unbroken Phase Protection due to Nonlinearities in 
PT-Symmetric Periodic Potentials

We have demonstrated that the interplay between a nonlinearity and PT symmetry in a periodic potential results in peculiar features of nonlinear periodic solutions. These include thresholdless symmetry breaking and asymmetric (multi-)loop structures of the nonlinear Bloch spectrum, persistence of unbroken PT symmetry even after the gap is closed, nonmonotonic dependence of the PT phase transition on the defocusing nonlinearity, and enhanced stability of the nonlinear states corresponding to the loop structures. The asymmetry and the loop structure of the spectrum have been explained within the framework of a two-mode approximation and an effective potential theory and been validated numerically.

Figure: The loop structure of the nonlinear Bloch spectrum for defocusing (upper row) and focusing [lower row, (b2)–(b5)] interactions for different strength V0 of the non-hermitian part of the Hamiltonian . Only the highest two Bloch bands are shown. The panels in the upper and lower rows from left to right correspond to V0={0,0.8,1.6,2,3} and V0={0.4,0.8,1.6,3,3.8}, respectively. In the shaded areas in panels (a5) and (b5), the spectrum is complex, i.e., PT symmetry is broken. Publication:
Asymmetric Loop Spectra and Unbroken Phase Protection due to Nonlinearities in 
PT-Symmetric Periodic Potentials
Yongping Zhang, Zhu Chen, Biao Wu, Thomas Busch, and Vladimir V. Konotop
Phys. Rev. Lett. 127, 034101 (2021)

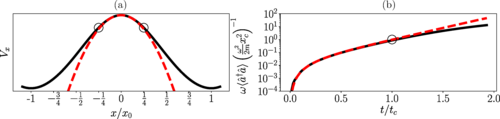
3.6 Inverted harmonic oscillator dynamics of the nonequilibrium phase transition in the Dicke model

We have shown how the dynamics of the Dicke model after a quench from the ground-state configuration of the normal phase into the superradiant phase can be described for a limited time by a simple inverted harmonic oscillator model and that this limited time approaches infinity in the thermodynamic limit. Although we have specifically discussed the Dicke model, the presented mechanism can also be used to describe dynamical quantum phase transitions in other systems and presents an opportunity for simulations of physical phenomena associated with an inverted harmonic oscillator.

Figure: Phenomenological condition for simulating the inverted oscillator with the Dicke model. (a) Effective double-well potential (black solid line) overlaid on an inverted oscillator potential (red dashed line). The black circles indicate the critical position up to which both models agree. (b) The critical position can be translated to a condition on the number of photons which can be related to a critical time for which the Dicke model can be used as a simulator. This time is indicated by the black circle. Publication:
Inverted harmonic oscillator dynamics of the nonequilibrium phase transition in the Dicke model
Karol Gietka and Thomas Busch
Phys. Rev. E 104, 034132 (2021)

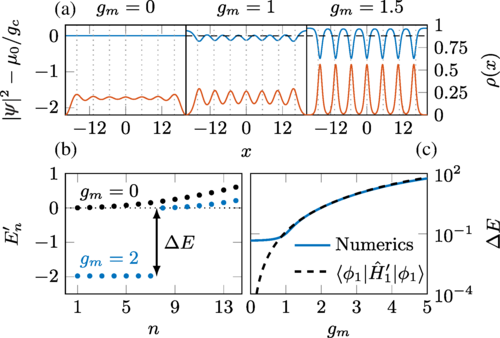
3.7 Self-Pinning Transition of a Tonks-Girardeau Gas in a Bose-Einstein Condensate

We have shown that a Tonks-Girardeau (TG) gas that is immersed in a Bose-Einstein condensate can undergo a transition to a crystal-like Mott state with regular spacing between the atoms without any externally imposed lattice potential. We have characterized this phase transition as a function of the interspecies interaction and temperature of the TG gas, and shown how it can be measured via accessible observables in cold atom experiments. We have also developed an effective model that accurately describes the system in the pinned insulator state and which allows one to derive the critical temperature of the transition.

Figure: (a) TG gas density ρ(x) (red lines) and BEC depletion |ψ|2−μ0/gc (blue lines) for N=7 TG atoms and increasing interaction strengths gm. The dotted lines indicate the maxima of the TG density in the noninteracting case gm=0. (b) Spectrum of the TG gas E′n=En−gmμ/gc for gm=0 (superfluid phase, black dots) and gm=2 (pinned phase, blue dots). (c) Size of the energy gap as a function of gm. The black dashed line shows an analytical approximation.  Publication:
Self-Pinning Transition of a Tonks-Girardeau Gas in a Bose-Einstein Condensate
Tim Keller, Thomás Fogarty, and Thomas Busch
Phys. Rev. Lett. 128, 053401 (2022). Editors' Suggestion

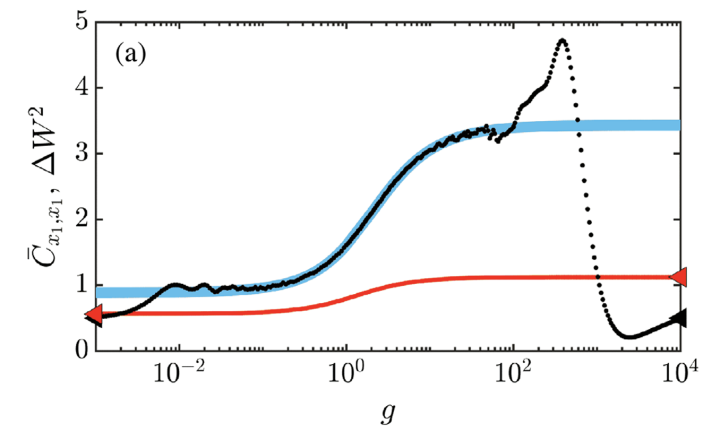
3.8 Connecting scrambling and work statistics for short-range interactions in the harmonic oscillator

We have investigated the relationship between information scrambling and work statistics after a quench for the paradigmatic example of short-range interacting particles in a one-dimensional harmonic trap, considering up to five particles numerically. In particular, we have found that scrambling requires finite interactions, in the presence of which the long-time average of the squared commutator for the individual canonical operators is directly proportional to the variance of the work probability distribution. We have also outline the mathematical structure of the N-body system which leads to this outcome and thereby established a connection between the scrambling properties and the induced work fluctuations, with the latter being an experimental observable that is directly accessible in modern cold-atom experiments.

Figure: The full blue line is the infinite-time average of the squared commutator Cx1,x1 as a function of g for γ=1/2. Black dots show the time average of the same squared commutator in an interval t∈[0,200π] as a function of g. The variance of the work distribution function ΔW2 is given by the red solid line. The triangles correspond to the g=0 and g=∞ values of Cxx (black) and ΔW2 (red). Publication:
Connecting scrambling and work statistics for short-range interactions in the harmonic oscillator
M. Mikkelsen, T. Fogarty, and Th. Busch
Phys. Rev. Lett. 128, 070605 (2022)

4. Publications

4.1 Journal

4.2 Books and other one-time publications

Nothing to report

4.3 Oral and Poster Presentations

4.3.1 Conference Oral Presentation

1. Fogarty, T. Cooperative effects in many-body heat engines, Tsung-Dao Lee Institute Youth Forum for Quantum Physics Tsung-Dao Lee Institute, China Onine, 10 January (2022)
2. Gietka, K. Critical Quantum Metrology Across the Superradiant Phase Transition, Quantum Optics and Information Meeting 6 (Kobit 6), Onine, 4 February (2022)
3. Metz, F. Self-Correcting Quantum Many-Body Control using Reinforcement Learning with Tensor Networks, AMLD EPFL 2022 Lausanne, Switzerland, 29 March (2022)

4.3.2 Conference Poster Presentation

1. Gietka, K., Ruks, L. and Busch, Th. Critical Quantum Metrology Across the Superradiant Phase Transition, 40+1 anniversary of Center for Theoretical Physics PAN Warsaw, Poland, 1 September (2021)
2. Gietka, K., Ruks, L. and Busch, Th. Critical Quantum Metrology Across the Superradiant Phase Transition, Quantum Optics X Toruń, Poland, 6 September (2021)
3. Keller, T., Fogarty, T. and Busch, Th.Self-Pinning Transition of a Tonks-Girardeau Gas in a Bose-Einstein Condensate, BEC 2021 Sant Feliu de Guixols, Spain, 11 Septermber (2021)
4. Keller, T., Fogarty, T. and Busch, Th. Self-pinning transition of a Tonks-Girardeau gas in a Bose-Einstein condensate, FermiPolar Workshop, Onine, 9 February (2022)
5. Morelli, S., Usui, A., Agudelo, E. and Friis, N. Spin-orbit coupling in the presence of strong atomic correlations Quantum Optics X Toruń, Poland, 6 Septermber (2021)
6. Usui, A., T Fogarty, T., Campbell,S., Gardiner, S. A. and Busch, Th. Spin-orbit coupling in the presence of strong atomic correlations, BEC 2021, Sant Feliu de Guixols, Spain 11 Septermber (2021)

4.3.3 Seminar

1. Gietka, K. Simulating the same physics with two distinct Hamiltonians,  Institute of Theoretical Physics, University of Innsbruck, Innsbruck, Austria Online, 19 May (2021)
2. Busch, Th. Magnetometry with Bose-Einstein condensates Institute of Theoretical Physics and Astronomy, Vilnius University, Lithuania 8 June (2021)
3. Busch, Th. Self-organisation in Bose-Einstein condensates, Kaiserlautern University, Germany, 8 September (2021)
4. Keller, T. Self-pinning transition of a Tonks-Girardeau gas in a Bose-Einstein condensate, Saarland University, Saarbrücken, Germany 8 October (2021)
5. Keller, T. Experimental considerations for the self-pinning transition, ETH Zurich, Zurich, Switzerland 11 October (2021)
6. Busch, Th. Self-organisation in Bose-Einstein condensates, Ulm University, 20 December (2021)
7. Ruks, L. Deriving equations for spin and center-of-mass for two-level atoms interacting through continuum media, University of Innsbruck, Online, 13 January (2022)
8. Ruks, L. Emission into structured bath (and simulation of dissipative spin systems), University of Lancaster, Online, 17 February (2022)

5. Intellectual Property Rights and Other Specific Achievements

Nothing to report

6. Seminar, Meetings and Events

6.1 Seminar

Nothing to report

6.2 Meetings and Events

6.2.1 OIST Quantum/Cyber Security Initiative

Kick-off Event: the Science, the Opportunities, and the Real-world Challenges

• Date: June 1 2021
• Venue: Webinar
• Speakers: Artur Ekert, Christopher Monroe, Michele Mosca
• Chair: Peter Gruss
• MCs: Kae Nemoto, Jesper Koll
• Organizers:
  • OIST Graduate University (President Offce, Busch U)
  • Asia Society Japan

6.2.2 OIST & ASJ Quantum/Cyber Security Seminar Series

Series 1 Satellite Quantum Communication and Impact on Cyber Security

• Date: November 9 2021
• Venue: Webinar
• Speaker: Alexander Ling
• Navigator: ArturEkert

Series 2 How will our cryptographic toolkit be impacted by quantum computers and machine learning?

• Date: January 28 2022
• Venue: Webinar
• Speaker: Najwa Aaraj
• Navigator: ArturEkert

Series 3 Privacy-Preserving Technologies: cryptographic techniques for secure computation

• Date: January 28 2022
• Venue: Webinar
• Speaker: Carlos Cid
• Navigator: Kae Nemoto

• Organizers:
  • OIST Graduate University　(President Offce, Busch U)
  • Asia Society Japan

7. Other

Nothing to report.