Validation
Singlephase flow
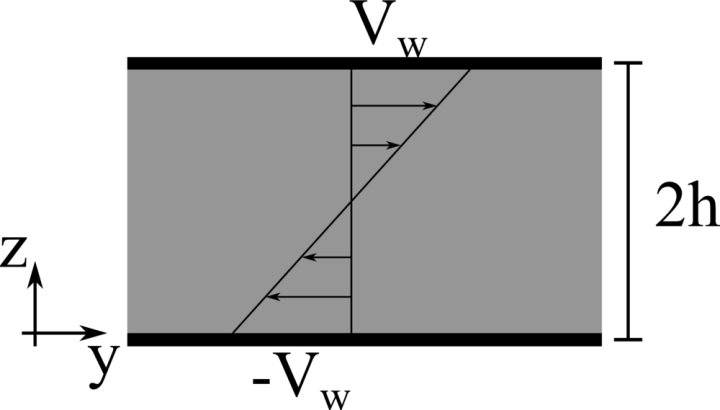
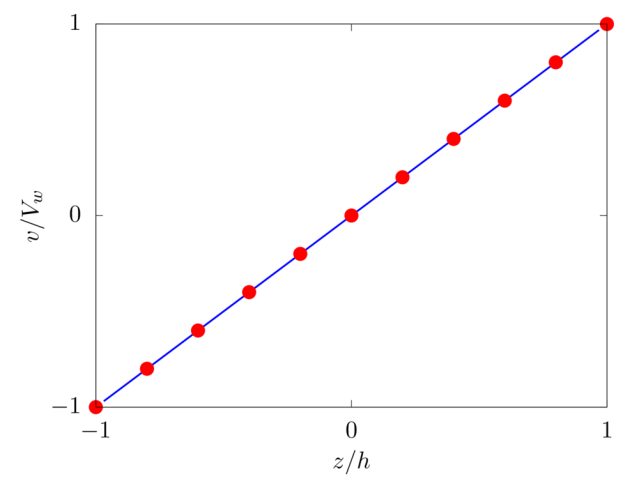
Laminar plane Couette flow
Analytical solution: v(z)=−Vw(1−z/h).
config.h
#define _FLOW_COUETTE_ #define _FLOW_INIT_LAMINAR_ #define _SOLVER_FFT2D_ #define _SINGLEPHASE_
parameters.f90
! Total number of grid points in X, Y and Z integer, parameter :: nxt = 4, nyt = 4, nzt = 32 ! Size of the domain in X, Y and Z real, parameter :: lx = 0.25, ly = 0.25, lz = 2.0 ! Fluid viscosity and density real, parameter :: vis = 0.1, rho = 1.0 ! Reference velocity (bulk velocity or wall velocity) real, parameter :: refVel = 1.0 ! Gravitational acceleration real, dimension(3), parameter :: gr=(/0.0,0.0,0.0/)
input/input.in
# Simulation initial and final steps 0 100 # Simulation initial time 0.0 # Simulation initial time-step 0.0002 # Output frequency: 0D, 1D, 2D, 3D, restart data 100 100 100 1000000 1000000 # Simulation restart condition for the multiphase part .false.
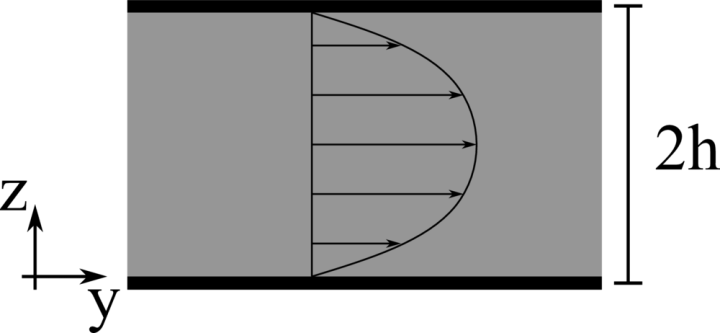
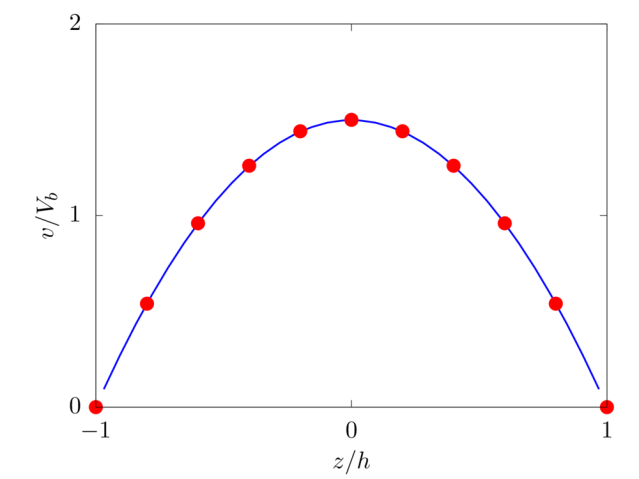
Laminar plane Poiseuille flow
Analytical solution: v(z)=6Vb(z/2h)[1−(z/2h)].
config.h
#define _FLOW_CHANNEL_ #define _FLOW_CHANNEL_CFR_ #define _FLOW_INIT_LAMINAR_ #define _SOLVER_FFT2D_ #define _SINGLEPHASE_
parameters.f90
! Total number of grid points in X, Y and Z integer, parameter :: nxt = 4, nyt = 4, nzt = 32 ! Size of the domain in X, Y and Z real, parameter :: lx = 0.25, ly = 0.25, lz = 2.0 ! Fluid viscosity and density real, parameter :: vis = 0.1, rho = 1.0 ! Reference velocity (bulk velocity or wall velocity) real, parameter :: refVel = 1.0 ! Gravitational acceleration real, dimension(3), parameter :: gr=(/0.0,0.0,0.0/)
input/input.in
# Simulation initial and final steps 0 100 # Simulation initial time 0.0 # Simulation initial time-step 0.0002 # Output frequency: 0D, 1D, 2D, 3D, restart data 100 100 100 1000000 1000000 # Simulation restart condition for the multiphase part .false.
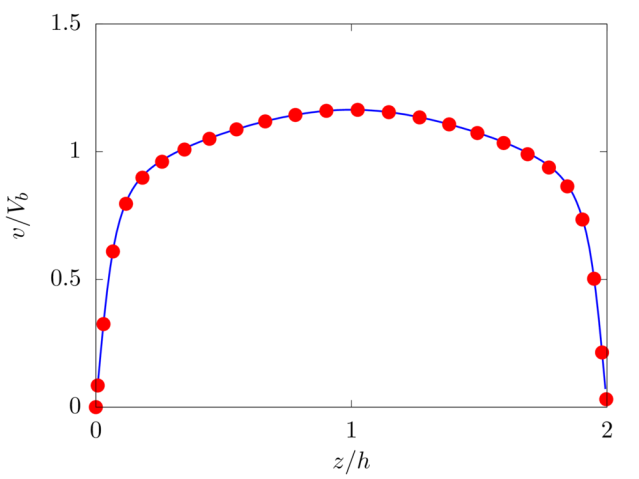
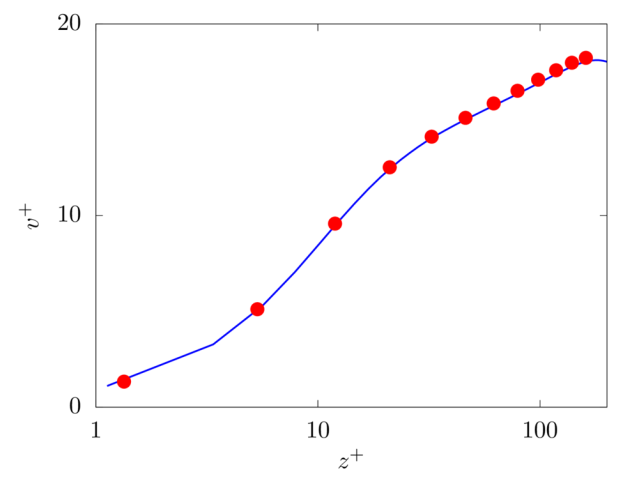
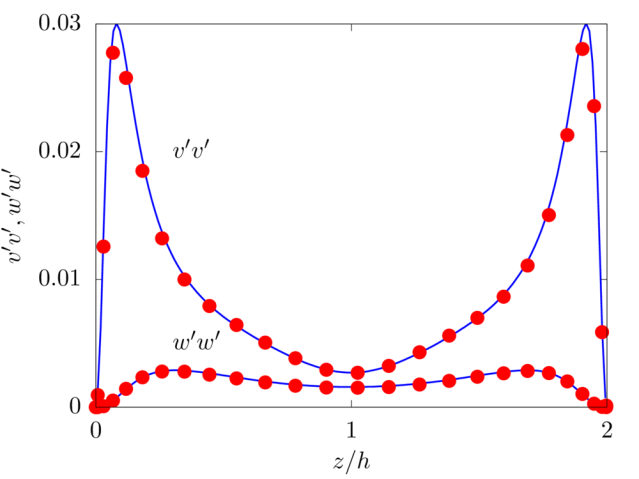
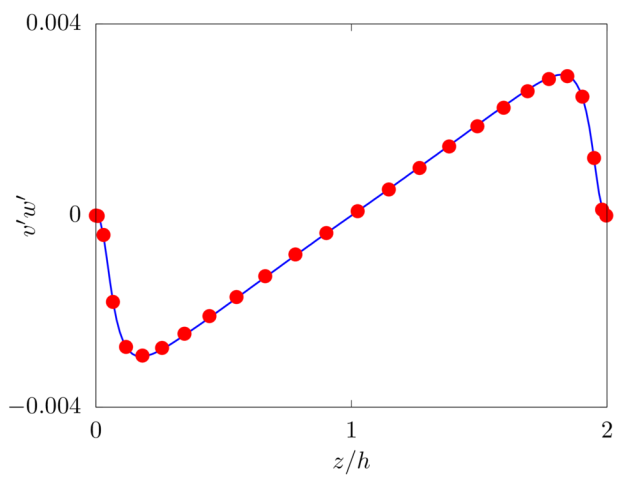
Turbulent plane channel flow
config.h
#define _FLOW_CHANNEL_ #define _FLOW_CHANNEL_CFR_ #define _FLOW_INIT_TURBULENT_ #define _SOLVER_FFT2D_ #define _SINGLEPHASE_
parameters.f90
! Total number of grid points in X, Y and Z integer, parameter :: nxt = 256, nyt = 512, nzt = 160 ! Size of the domain in X, Y and Z real, parameter :: lx = 3.0, ly = 6.0, lz = 2.0 ! Fluid viscosity and density real, parameter :: vis = 2.0/5600.0, rho = 1.0 ! Reference velocity (bulk velocity or wall velocity) real, parameter :: refVel = 1.0 ! Gravitational acceleration real, dimension(3), parameter :: gr=(/0.0,0.0,0.0/)
input/input.in
# Simulation initial and final steps 0 9999999 # Simulation initial time 0.0 # Simulation initial time-step 0.002 # Output frequency: 0D, 1D, 2D, 3D, restart data 100 1000 2000 1000000 10000 # Simulation restart condition for the multiphase part .false.
ABC flow
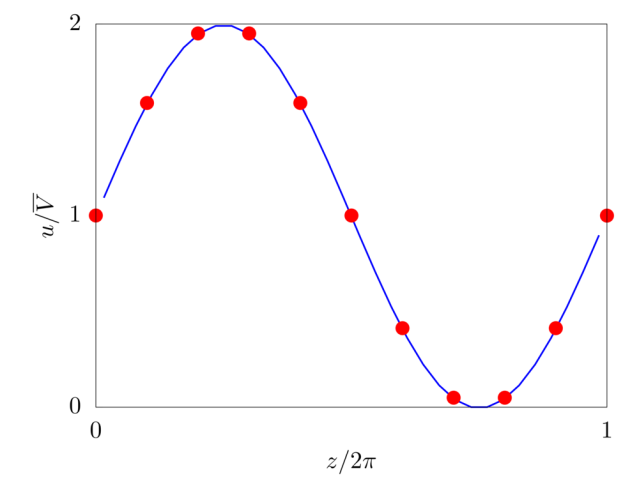
We consider the Arnold-Beltrami-Childress (ABC) flow in a three-periodic domain of size 2πL. The velocity field is initialized as
u=¯V[sin(z/L)+cos(y/L)],
v=¯V[sin(x/L)+cos(z/L)],
w=¯V[sin(y/L)+cos(x/L)].
The Reynolds number Re=ρ¯VL/μ is fixed equal to 10 and 32 grid points per side are used to discretise the numerical domain.
config.h
#define _FLOW_TRIPERIODIC_ #define _FLOW_TRIPERIODIC_ABC_ #define _FLOW_INIT_LAMINAR_ #define _SOLVER_FFT3D_ #define _SINGLEPHASE_
parameters.f90
! Total number of grid points in X, Y and Z integer, parameter :: nxt = 32, nyt = 32, nzt = 32 ! Size of the domain in X, Y and Z real, parameter :: lx = 2.0*acos(-1.), ly = 2.0*acos(-1.), lz = 2.0*acos(-1.) ! Fluid viscosity and density real, parameter :: vis = 0.1, rho = 1.0 ! Reference velocity (bulk velocity or wall velocity) real, parameter :: refVel = 1.0 ! Gravitational acceleration real, dimension(3), parameter :: gr=(/0.0,0.0,0.0/)
input/input.in
# Simulation initial and final steps 0 100 # Simulation initial time 0.0 # Simulation initial time-step 0.0002 # Output frequency: 0D, 1D, 2D, 3D, restart data 100 100 100 1000000 1000000 # Simulation restart condition for the multiphase part .false.
Taylor-Green Vortex
We consider the time evolution of a Taylor-Green vortex in a three-periodic domain of size 2πL. The velocity field is initialized as
u=Usin(x/L)cos(y/L)cos(z/L),
v=−Ucos(x/L)sin(y/L)cos(z/L),
w=0.
The Reynolds number Re=ρUL/μ is fixed equal to 1600 and 512 grid points per side are used to discretise the numerical domain.
config.h
#define _FLOW_TRIPERIODIC_ #define _FLOW_TRIPERIODIC_TGV_ #define _FLOW_INIT_LAMINAR_ #define _SOLVER_FFT3D_ #define _SINGLEPHASE_
parameters.f90
! Total number of grid points in X, Y and Z integer, parameter :: nxt = 512, nyt = 512, nzt = 512 ! Size of the domain in X, Y and Z real, parameter :: lx = 2.0*acos(-1.), ly = 2.0*acos(-1.), lz = 2.0*acos(-1.) ! Fluid viscosity and density real, parameter :: vis = 1.0/1600.0, rho = 1.0 ! Reference velocity (bulk velocity or wall velocity) real, parameter :: refVel = 1.0 ! Gravitational acceleration real, dimension(3), parameter :: gr=(/0.0,0.0,0.0/)
input/input.in
# Simulation initial and final steps 0 9999999 # Simulation initial time 0.0 # Simulation initial time-step 0.0002 # Output frequency: 0D, 1D, 2D, 3D, restart data 100 1000000 1000000 1000000 10000 # Simulation restart condition for the multiphase part .false.
Homogeneous Isotropic Turbulence
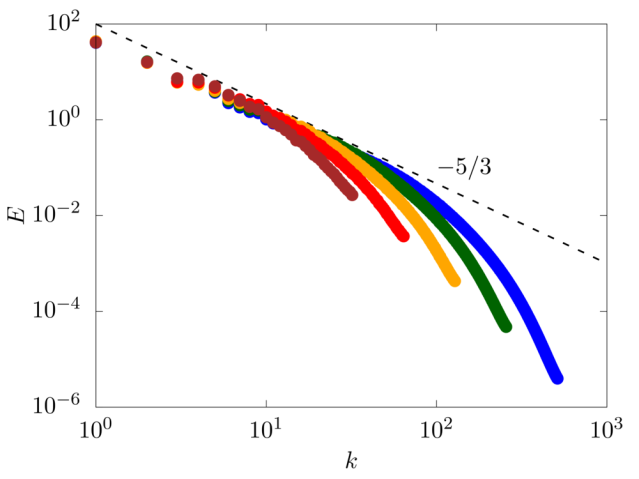
We consider an homogeneous isotropic turbulent flow in a three-periodic domain of size 2πL. The flow is sustained by a random forcing in Fourier space [4] on wave numbers within a shell of radius k=2. The Taylor microscale Reynolds number Re=ρu′λ/μ is varied from 100 to 400, and 64, 128, 256, 512 and 1024 grid points per side are used to discretise the numerical domain.
config.h
#define _FLOW_TRIPERIODIC_
#define _FLOW_TRIPERIODIC_ISO_
#define _FLOW_INIT_LAMINAR_
#define _SOLVER_FFT3D_
#define _SINGLEPHASE_
parameters.f90
! Total number of grid points in X, Y and Z integer, parameter :: nxt = 1024, nyt = 1024, nzt = 1024 ! Size of the domain in X, Y and Z real, parameter :: lx = 2.0*acos(-1.), ly = 2.0*acos(-1.), lz = 2.0*acos(-1.) ! Fluid viscosity and density real, parameter :: vis = 1.0/400.0, rho = 1.0 ! Reference velocity (bulk velocity or wall velocity) real, parameter :: refVel = 1.0 ! Gravitational acceleration real, dimension(3), parameter :: gr=(/0.0,0.0,0.0/)
input/input.in
# Simulation initial and final steps 0 9999999 # Simulation initial time 0.0 # Simulation initial time-step 0.00001 # Output frequency: 0D, 1D, 2D, 3D, restart data 100 1000000 1000000 1000000 10000 # Simulation restart condition for the multiphase part .false.
References:
[1] D. S. Henningson and J. Kim. On turbulent spots in plane poiseuille flow. Journal of Fluid Mechanics, 228:183–205, 1991.
[2] J. Kim, P. Moin, and R. Moser. Turbulence statistics in fully developed channel flow at low Reynolds number. Journal of Fluid Mechanics, 177:133–166, 1987.
[3] W. M. Van Rees, A. Leonard, D. I. Pullin, and P. Koumoutsakos. A comparison of vortex and pseudo- spectral methods for the simulation of periodic vortical flows at high reynolds numbers. Journal of Computational Physics, 230(8):2794–2805, 2011.
[4] V. Eswaran and S. B. Pope. An examination of forcing in direct numerical simulations of turbulence. Computers & Fluids, 16(3):257–278, 1988.
VOF
Buoyancy-driven flow
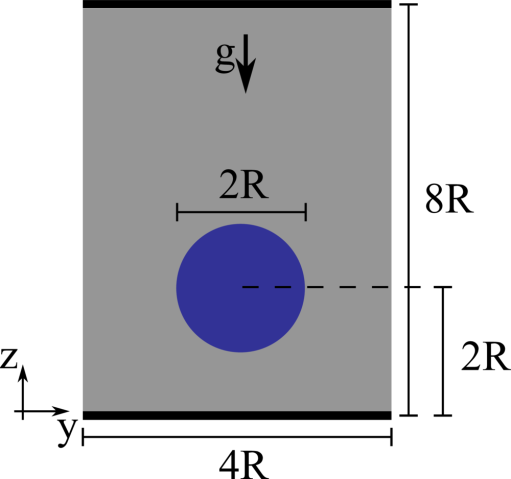
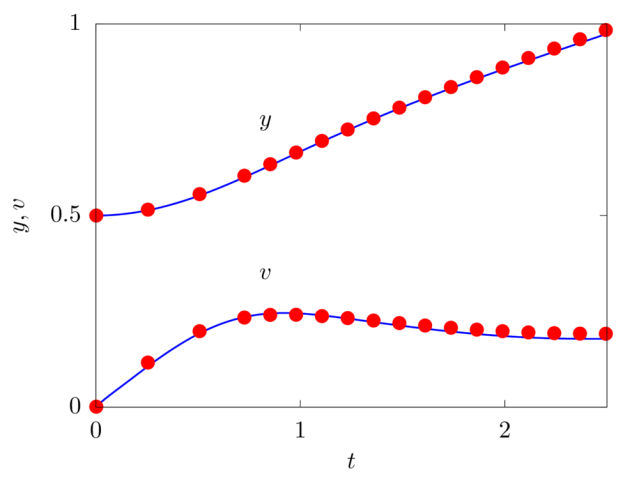
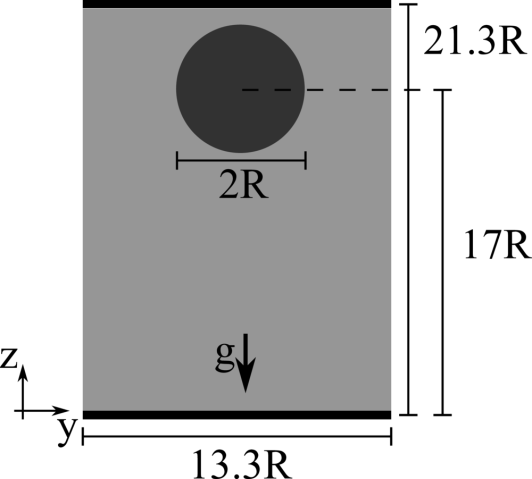
We consider a 2D droplet of radius R rising in a fluid with different density and viscosity. The droplet has viscosity μ1 and density and ρ1, while the surrounding fluid has viscosity μ2 and density ρ2, providing a viscosity and density ratio equal to kμ=10 and kρ=10. The two fluids are separted by an interface with interfacial surface tension σ. The domain is rectangular with size 4R×8R, no-slip boundary conditions are applied on the horizontal walls and free-slip boundary conditions on the sides. The droplet is initially round and placed at the centerline of the channel at a distance of 2R from the bottom wall. The non-dimensional parameters governing the flow are the Reynolds number Re=ρ1Ug2R/μ1 equal to 35, the Eotvos number Eo=ρ1U2g2R/σ equal to 10, and the Capillary number Ca=μ1Ug/σ equal to 0.2875, where Ug=√g2R being g the gravitational acceleration.
config.h
#define _FLOW_COUETTE_ #define _SOLVER_FFT2D_ #define _MULTIPHASE_ #define _MULTIPHASE_VOF_ #define _MULTIPHASE_VOF_DROPLETS_ #define _MULTIPHASE_VISCOSITY_VARIABLE_ #define _MULTIPHASE_DENSITY_VARIABLE_ #define _MULTIPHASE_VOF_2D_ #define _MULTIPHASE_VOF_QUADRATIC_
param.f90
!Total number of grid points in X, Y and Z integer, parameter :: nxt = 4, nyt = 128, nzt = 256 !Size of the domain in X, Y and Z real, parameter :: lx = 4.0*1.0/128.0, ly = 1.0, lz = 2.0 !Fluid viscosity and density real, parameter :: vis = 10.0, rho = 1000.0 !Reference velocity (bulk velocity or wall velocity) real, parameter :: refVel = 0.0 !Gravitational acceleration real, dimension(3), parameter :: gr=(/0.0,0.0,-0.98/) !Output frequency integer,parameter :: iout0d = 100, iout1d = 10000, iout2d = 10000, iout3d = 10000, ioutfld = 10000 !Number of droplets integer, parameter :: vofN = 1 !Interfacial surface tension real, parameter :: vofSigma = 24.5 !Viscosity of the disphersed phase (phi=1) real, parameter :: vofVis1 = 1.0 !Viscosity of the carrier phase (phi=0) real, parameter :: vofVis2 = vis !Density of the disphersed phase (phi=1) real, parameter :: vofRho1 = 100.0 !Density of the carrier phase (phi=0) real, parameter :: vofRho2 = rho
main.f90
! Simulation initial step iStart = 0 ! Simulation final step iEnd = 9999999 ! Choose the timestep dt = 0.00001
initDropletPosition.dat
0.5 0.5 0.25
Droplet deformation in a shear flow
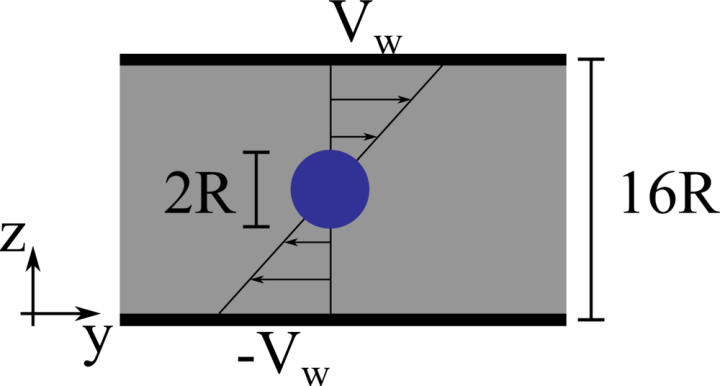
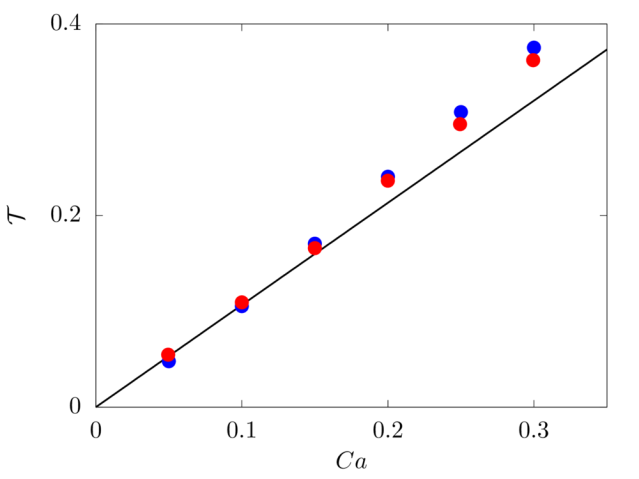
We consider a 3D spherical drop of radius R located at the center of a computational domain of size 8R×16R×16R, discretised with a resolution of 20 grid points per drop diameter. The top and bottom walls move with opposite velocity ±Vw, providing a shear rate ˙γ=2Vw/16R, while periodic boundary conditions are imposed in the remaining directions. The same density and viscosity are specified for the spherical drop and the surrounding fluid, the Reynolds number Re=ρ˙γR2/μ is fixed to 0.1, and six capillary numbers are studied: 0.05, 0.10, 0.15, 0.20, 0.25 and 0.30.
config.h
#define _FLOW_COUETTE_ #define _SOLVER_FFT2D_ #define _MULTIPHASE_ #define _MULTIPHASE_VOF_ #define _MULTIPHASE_VOF_DROPLETS_ #define _MULTIPHASE_VISCOSITY_UNIFORM_ #define _MULTIPHASE_DENSITY_UNIFORM_ #define _MULTIPHASE_VOF_3D_ #define _MULTIPHASE_VOF_QUADRATIC_
param.f90
!Total number of grid points in X, Y and Z integer, parameter :: nxt = 80, nyt = 160, nzt = 160 !Size of the domain in X, Y and Z real, parameter :: lx = 4.0, ly = 8.0, lz = 8.0 !Fluid viscosity and density real, parameter :: vis = 0.5**2/0.1, rho = 1.0 !Reference velocity (bulk velocity or wall velocity) real, parameter :: refVel = 4.0 !Gravitational acceleration real, dimension(3), parameter :: gr=(/0.0,0.0,-0.0/) !Output frequency integer,parameter :: iout0d = 100, iout1d = 100000, iout2d = 20000, iout3d = 100000, ioutfld = 100000 !Number of droplets integer, parameter :: vofN = 1 !Interfacial surface tension real, parameter :: vofSigma = vis*0.5/0.05
main.f90
! Simulation initial step iStart = 0 ! Simulation final step iEnd = 9999999 ! Choose the timestep dt = 0.0001/2.0
initDropletPosition.dat
2.0 4.0 4.0 0.5
References:
[1] S. R. Hysing, S. Turek, D. Kuzmin, N. Parolini, E. Burman, S. Ganesan, and L. Tobiska. Quantitative benchmark computations of two-dimensional bubble dynamics. International Journal for Numerical Methods in Fluids, 60(11):1259-1288, 2009.
[2] S. Ii, K. Sugiyama, S. Takeuchi, S. Takagi, Y. Matsumoto, and F. Xiao. An interface capturing method with a continuous function: the THINC method with multi-dimensional reconstruction. Journal of Computational Physics, 231(5):2328–2358, 2012.
[3] G. I. Taylor. The formation of emulsions in definable fields of flow. Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, 146(858):501–523, 1934.
IBM - Rigid particle
Uniform flow around a cylinder
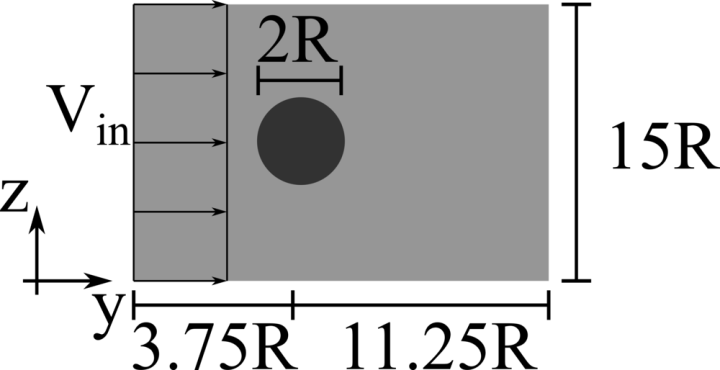
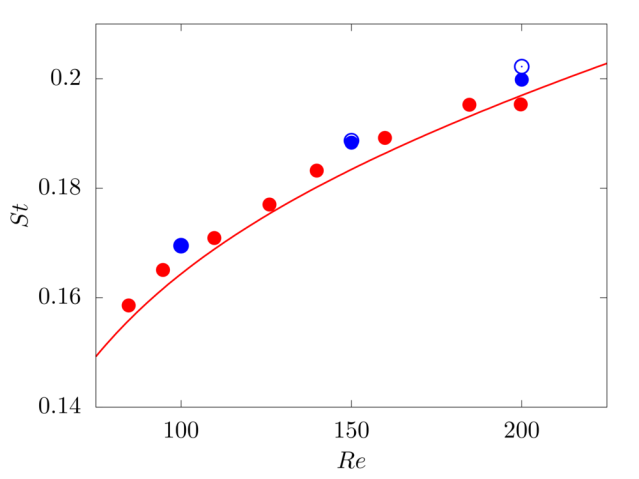
We consider a 2D rigid cylinder of radius R located in a computational domain of size 15R×15R, discretised with a resolution of 68 grid points per particle diameter. The incoming flow is uniform with velocity Vin, providing a Reynolds number Re=DVin/ν of 100, 150 and 200.
config.h
#define _FLOW_COUETTE_ #define _FLOW_INOUT_ #define _FLOW_INOUT_UNBOUND_ #define _SOLVER_INOUT_ #define _MULTIPHASE_ #define _MULTIPHASE_IBM_ #define _MULTIPHASE_IBM_2D_
param.f90
! Total number of grid points in X, Y and Z integer, parameter :: nxt = 4, nyt = 2048, nzt = 2048 ! Size of the domain in X, Y and Z real, parameter :: lx = 30.0/2048.*4., ly = 30.0, lz = 30.0 ! Fluid viscosity and density real, parameter :: vis = 1.0/200.0 real, parameter :: rho = 1.0 ! Reference velocity (bulk velocity or wall velocity) real, parameter :: refVel = 1.0 !Gravitational acceleration real, dimension(3), parameter :: gr=(/0.0,0.0,-0.0/) ! Number of particles integer, parameter :: ibmN = 1 ! Particle radius and density real, parameter :: ibmR = 0.5, ibmRho = 1.0, ibmRhoF = rho
input/input.in
# Simulation initial and final step 1200000 9999999 # Simulation time 299.99999999463392 # Simulation time-step 2.5000000000000001E-004 # Output frequency 400 1000000 40000 1000000 400000 # Simulation restart condition for the multiphase part F
initParticlePosition.dat
7.5 15.0
Lateral migration of a circular cylinder in a shear flow
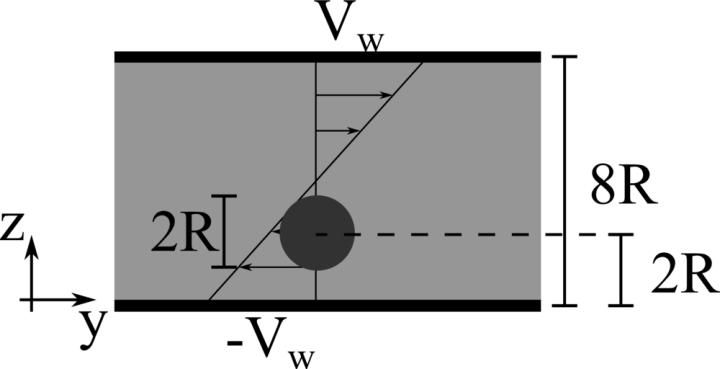
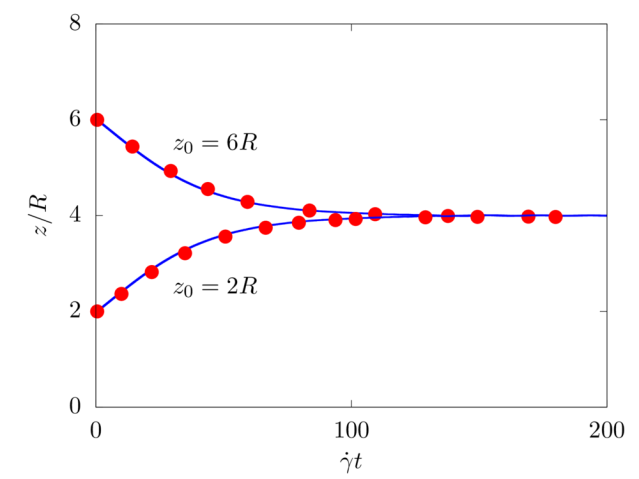
We consider a 2D rigid cylinder of radius R located in a computational domain of size 8R×50R, discretised with a resolution of 16 grid points per particle diameter. The top and bottom walls move with opposite velocity ±Vw, providing a shear rate ˙γ=2Vw/8R, while periodic boundary conditions are imposed in the remaining directions. The particle is neutrally buoyant, and the Reynolds number Re=ρ˙γR2/μ is fixed equal to 40. Two different initial conditions are studied: z=2R and 6R.
config.h
#define _FLOW_COUETTE_ #define _SOLVER_FFT2D_ #define _MULTIPHASE_ #define _MULTIPHASE_IBM_ #define _MULTIPHASE_IBM_2D_
param.f90
!Total number of grid points in X, Y and Z integer, parameter :: nxt = 4, nyt = 8*50, nzt = 8*8 !Size of the domain in X, Y and Z real, parameter :: lx = 4.0/8.0, ly = 50.0, lz = 8.0 !Fluid viscosity and density real, parameter :: vis = 1.0*8.0/40.0, rho = 1.0 !Reference velocity (bulk velocity or wall velocity) real, parameter :: refVel = 0.5 !Gravitational acceleration real, dimension(3), parameter :: gr=(/0.0,0.0,-0.0/) !Output frequency integer,parameter :: iout0d = 20, iout1d = 1000000, iout2d = 4000, iout3d = 1000000, ioutfld = 1000000 integer, parameter :: ibmN=1 real, parameter :: ibmR=1.0, ibmRhoF=rho, ibmRho=ibmRhoF, ibmVol=pi*ibmR**2, ibmMas=ibmRho*ibmVol, ibmIne=0.5*ibmMas*ibmR**2
main.f90
!Simulation initial step iStart = 0 !Simulation final step iEnd = 9999999 !Choose the timestep dt = 0.000001
initParticlePosition.dat
0.5 2.0
Lateral migration of a circular cylinder in a pressure driven flow
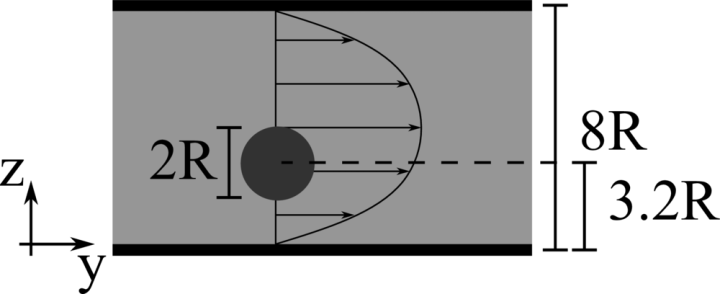
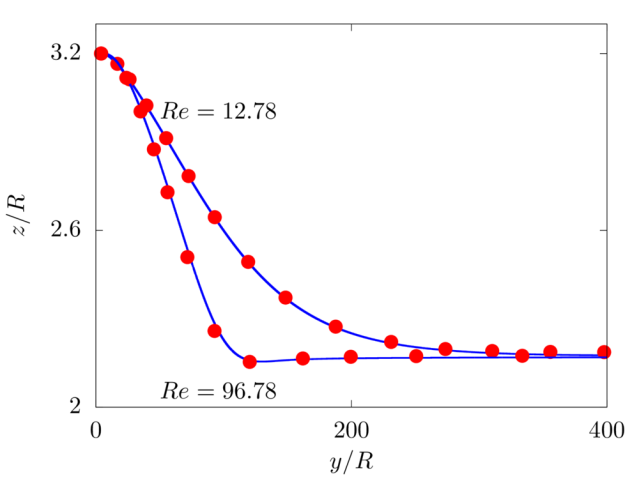
We consider a 2D rigid cylinder of radius R located in a computational domain of size 8R×8R, discretised with a resolution of 32 grid points per particle diameter. The flow is driven by an imposed pressure gradient, such that the resulting Reynolds number Re=ρVb8R/μ is equal to 12.78 and 96.74. The particle is neutrally buoyant and initially located at 3.2R from the bottom wall.
config.h
#define _FLOW_CHANNEL_ #define _FLOW_CHANNEL_CPG_ #define _SOLVER_FFT2D_ #define _MULTIPHASE_ #define _MULTIPHASE_IBM_ #define _MULTIPHASE_IBM_2D_
param.f90
!Total number of grid points in X, Y and Z integer, parameter :: nxt = 4, nyt = 256, nzt = 256 !Size of the domain in X, Y and Z real, parameter :: lx = 1.0/128.0*4.0/2.0, ly = 1.0, lz = 1.0 !Fluid viscosity and density real, parameter :: vis = 4.283E-04, rho = 1.0 !Reference velocity (bulk velocity or wall velocity) real, parameter :: refVel = 0.0 !Imposed pressure gradient real, parameter :: gradP = 2.337E-04 !Gravitational acceleration real, dimension(3), parameter :: gr=(/0.0,0.0,-0.0/) !Output frequency integer,parameter :: iout0d = 20, iout1d = 1000000, iout2d = 4000, iout3d = 1000000, ioutfld = 1000000 integer, parameter :: ibmN=1 real, parameter :: ibmR=0.125, ibmRhoF=rho, ibmRho=ibmRhoF, ibmVol=pi*ibmR**2, ibmMas=ibmRho*ibmVol, ibmIne=0.5*ibmMas*ibmR**2
main.f90
!Simulation initial step iStart = 0 !Simulation final step iEnd = 9999999 !Choose the timestep dt = 0.001
initParticlePosition.dat
0.5 0.4
Sedimentation of a spherical particle
We consider a rectangular domain filled with a liquid with density and viscosity equal to 960kg m−3 and 0.058Pa s. The domain size is 0.1m×0.1m×0.16m in the x, y and z directions, where x and y are the two horizontal directions, while z is the vertical direction parallel to the gravitational acceleration g=9.81m s−2. A particle of diameter 0.015m and density 1120kg m−3 is initially positioned at (0.05m,0.05m,0.1275m).
config.h
#define _FLOW_CHANNEL_ #define _FLOW_CHANNEL_CPG_ #define _SOLVER_FFT2D_ #define _MULTIPHASE_ #define _MULTIPHASE_IBM_ #define _MULTIPHASE_IBM_3D_
param.f90
!Total number of grid points in X, Y and Z integer, parameter :: nxt = 192, nyt = 192, nzt = 304 !Size of the domain in X, Y and Z real, parameter :: lx = 0.1, ly = 0.1, lz = 0.1/192.0*304.0 !Fluid viscosity and density real, parameter :: vis = 0.058, rho = 960.0 !Reference velocity (bulk velocity or wall velocity) real, parameter :: refVel = 0.0 !Imposed pressure gradient real, parameter :: gradP = 0.0 !Gravitational acceleration real, dimension(3), parameter :: gr=(/0.0,0.0,-9.8/) !Output frequency integer,parameter :: iout0d = 20, iout1d = 1000000, iout2d = 1000000, iout3d = 1000000, ioutfld = 1000000 integer, parameter :: ibmN=1 real, parameter :: ibmR = 0.015/2.0, ibmRhoF = rho, ibmRho = 1120.0
main.f90
!Simulation initial step iStart = 0 !Simulation final step iEnd = 9999999 !Choose the timestep dt = 0.0001
initParticlePosition.dat
0.05 0.05 0.1275
References:
[1] C. H. K. Williamson. Defining a universal and continuous Strouhal-Reynolds number relationship for the laminar vortex shedding of a circular cylinder. Physics of Fluids, 31(10):2742–2744, 1988.
[2] E. Guilmineau and P. Queutey. A numerical simulation of vortex shedding from an oscillating circular cylinder. Journal of Fluids and Structures, 16(6):773–794, 2002.
[3] J. Feng, H. H. Hu, and D. D. Joseph. Direct simulation of initial value problems for the motion of solid bodies in a newtonian fluid. part 2. couette and poiseuille flows. Journal of Fluid Mechanics, 277:271–301, 1994.
[4] T. W. Pan and R. Glowinski. Direct simulation of the motion of neutrally buoyant circular cylinders in plane poiseuille flow. Journal of Computational Physics, 181(1):260–279, 2002.
[5] A. Ten Cate, C. H. Nieuwstad, J. J. Derksen, and H. E. A. Van den Akker. Particle imaging velocimetry experiments and lattice-boltzmann simulations on a single sphere settling under gravity. Physics of Fluids, 14(11):4012–4025, 2002.
IBM - Flexible fiber
Free vibration of unsupported and cantilevered fibers
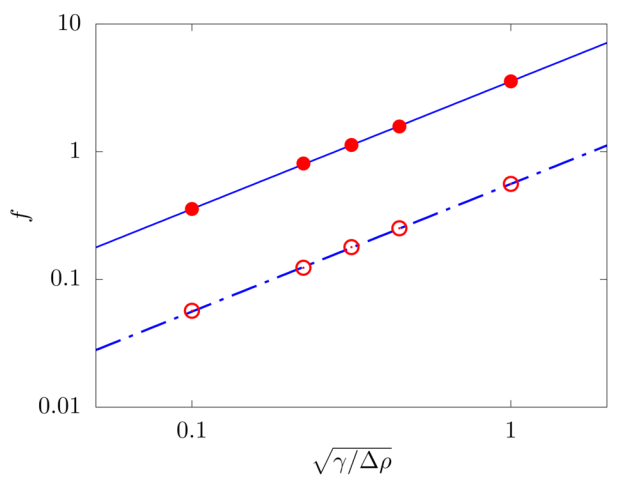
In the absence of any load, we evaulate the free vibration of a fiber. The filament length c, flexibility γ and linear density difference Δ˜ρ are varied and the resulting frequency f of the free oscillations measured. The filament is discretised with 100 Lagrangian points.
Analytical solution - free: f=22.37332πc2√γΔ˜ρ
Analytical solution - clamped: f=3.51612πc2√γΔ˜ρ
config.h
#define _FLOW_CHANNEL_ #define _FLOW_FIXED_ #define _MULTIPHASE_ #define _MULTIPHASE_FIL_ #define _MULTIPHASE_FIL_FREE_ #define _MULTIPHASE_FIL_FIXD_
param.f90
! Gravitational acceleration real, dimension(3), parameter :: gr=(/0.0,0.0,0.0/) ! Number of filaments integer, parameter :: filN=1 ! Number of Lagrangian points per filament integer, parameter :: filNL=100 ! Length of the filaments real, parameter :: filL = 1.0 ! Filament linear density difference and flexibility real, parameter :: filDRhoL = 1.0, filGamma=0.01
input/input.in
# Simulation initial and final step 0 200000 # Simulation time 0.0 # Simulation time-step 1.0000000000000001E-004 # Output frequency 1 100000 100 1000000 1000000 # Simulation restart condition for the multiphase part F
A hanging filament under gravity
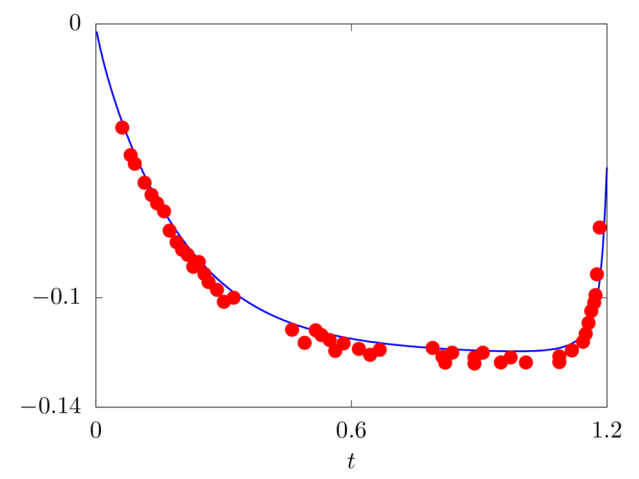
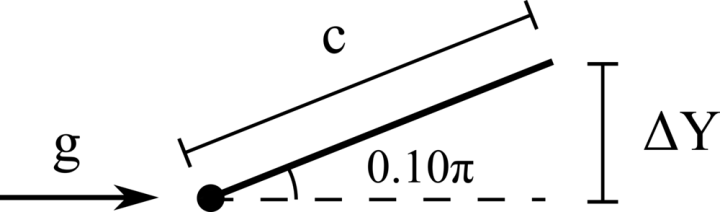
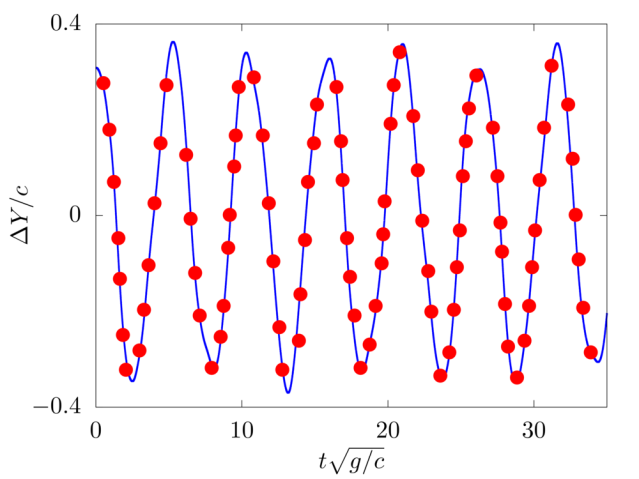
We consider the oscillations of a hanging filament under gravity. A filament of length c=1m, linear density difference Δ˜ρ=1kg/m and flexibility γ=0.01kg m3/s2 is initially held stationary with an angle of 0.1π from the vertical and then, after being released, starts swinging due to the gravity force g=10m/s2. The filament is discretised with 100 Lagrangian points.
config.h
#define _FLOW_CHANNEL_ #define _FLOW_FIXED_ #define _MULTIPHASE_ #define _MULTIPHASE_FIL_ #define _MULTIPHASE_FIL_HING_ #define _MULTIPHASE_FIL_FIXD_
param.f90
! Gravitational acceleration real, dimension(3), parameter :: gr=(/0.0,10.0,0.0/) ! Number of filaments integer, parameter :: filN=1 ! Number of Lagrangian points per filament integer, parameter :: filNL=100 ! Length of the filaments real, parameter :: filL = 1.0 ! Filament linear density difference and flexibility real, parameter :: filDRhoL = 1.0, filGamma=0.01
input/input.in
# Simulation initial and final step 0 200000 # Simulation time 0.0 # Simulation time-step 1.0000000000000001E-004 # Output frequency 1 100000 100 1000000 1000000 # Simulation restart condition for the multiphase part F
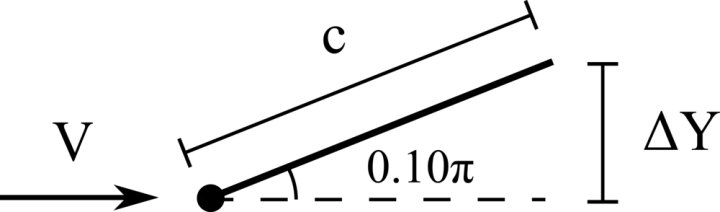
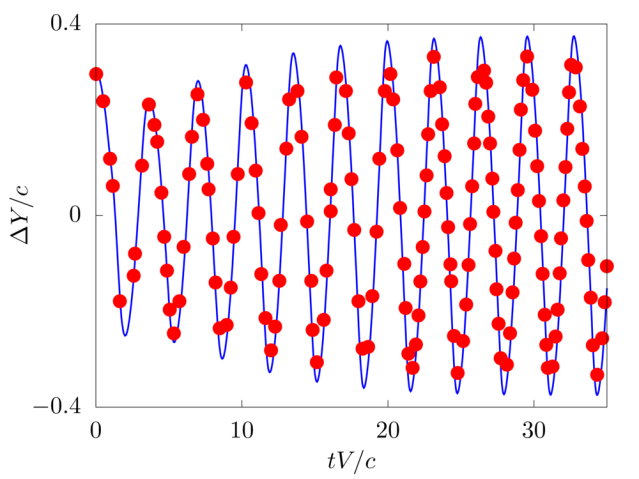
A hanging filament in a uniform flow
We consider the oscillations of a hanging filament in a uniform flow with velocity V. A filament of length c=1m, linear density difference Δ˜ρ=1.5kg/m and flexibility γ=0.0015kg m3/s2 is initially held stationary with an angle of 0.1π from the vertical and then, after being released, starts swinging due to the combined effect of the viscous fluid flow (ν=0.005m2/s) and gravity force (g=0.5m/s2). The filament is discretised with 65 Lagrangian points.
config.h
#define _FLOW_INOUT_ #define _FLOW_INOUT_UNBOUND_ #define _SOLVER_INOUT_ #define _MULTIPHASE_ #define _MULTIPHASE_IBML_ #define _MULTIPHASE_IBML_GLDS_ #define _MULTIPHASE_IBML_GLDS_2D_ #define _MULTIPHASE_IBML_XXXX_READ_ #define _MULTIPHASE_IBML_XXXX_FIL_ #define _MULTIPHASE_IBML_XXXX_FIL_HING_
param.f90
! Fluid viscosity and density real, parameter :: vis = 1.0/200.0 real, parameter :: rho = 1.0 ! Reference velocity (bulk velocity or wall velocity) real, parameter :: refVel = 1.0 ! Gravitational acceleration real, dimension(3), parameter :: gr=(/0.0,0.5,0.0/) ! Number of objects integer, parameter :: ibmlN=1 ! Number of Lagrangian points per object integer, parameter :: ibmlNL=65 ! Linear dimension of the object real, parameter :: ibmlL = 1.0 ! Moving or not object logical, parameter :: ibmlMoving = .TRUE. ! Filament linear density difference and flexibility real, parameter :: filDRhoL = 1.5, filGamma=1e-3*filDRhoL
input/input.in
# Simulation initial and final step 0 100000 # Simulation time 0.0 # Simulation time-step 5.0E-004 # Output frequency: 0D, 1D, 2D, 3D, restart data 100 10000 100000 1000000 2000000 # Simulation restart condition for the multiphase part F
References:
[1] W. X. Huang, S. J. Shin, and H. J. Sung. Simulation of flexible filaments in a uniform flow by the immersed boundary method. Journal of Computational Physics, 226(2):2206–2228, 2007.
Non-Newtonian fluid
We consider the pressure-driven flow of a viscous fluid in a channel, i.e., a plane Poiseuille flow. x, y, and z denote the spanwise, streamwise, and wall-normal coordinates, while u, v, and w the corresponding components of the velocity vector field. The lower and upper impermeable walls are located at z=−h and z=h, respectively, and the flow is driven by a uniform pressure gradient in the streamwise direction Py. The pressure gradient is such that with a Newtonian fluid the centerline velocity Vc=Pyh2/2μ is equal to 1. 32 grid points are used to discretise the domain in the wall-normal direction. Different non-Newtonian fluids are considered.
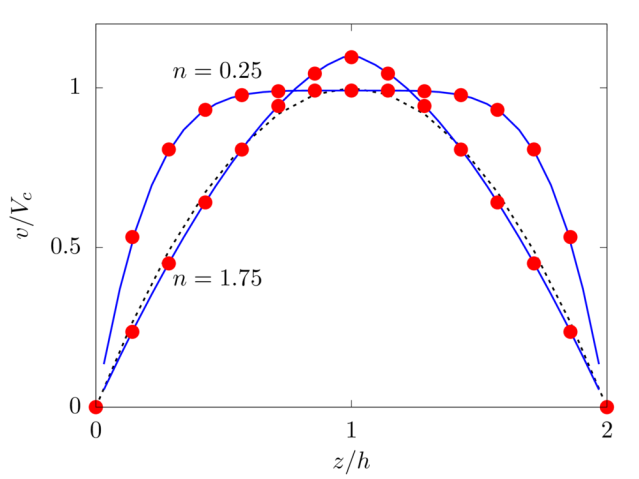
Power-law fluid
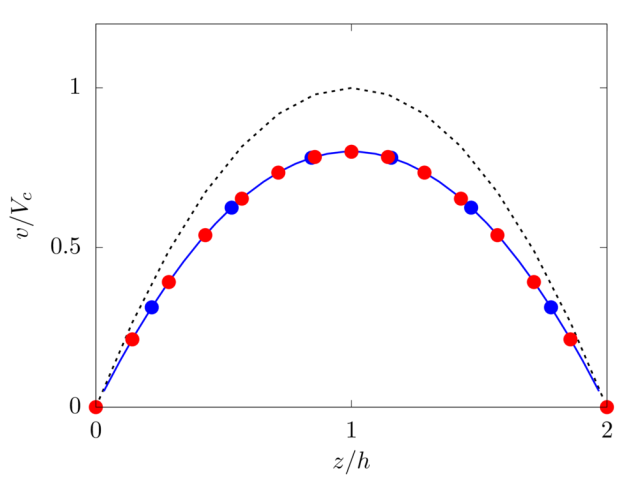
We consider shear-thinning and thickening fluids modeled as simple power-law fluids with local viscosity μl=k˙γn−1, with power index n=0.75 and 1.75, respectively, and fluid consistency index k such that μl(˙γ0)=μ, being ˙γ0 the mean shear rate in the channel for a Newtonian fluid, i.e. Py/2μh.
Analytical solution: v(z)=nn+1(Pyk)1n[hn+1n−(z−h)n+1n].
config.h
#define _FLOW_CHANNEL_ #define _FLOW_CHANNEL_CPG_ #define _FLOW_CHANNEL_LAMINAR_ #define _SOLVER_FFT2D_ #define _MULTIPHASE_ #define _MULTIPHASE_NNF_ #define _MULTIPHASE_VISCOSITY_VARIABLE_ #define _MULTIPHASE_DENSITY_UNIFORM_ #define _MULTIPHASE_NNF_POW_ #define _MULTIPHASE_NNF_POW_C_
param.f90
! Total number of grid points in X, Y and Z integer, parameter :: nxt = 4, nyt = 4, nzt = 32 ! Size of the domain in X, Y and Z real, parameter :: lx = 0.25, ly = 0.25, lz = 2.0 ! Fluid viscosity and density real, parameter :: vis = 0.01, rho = 1.0 ! Imposed pressure gradient real, parameter :: gradP = 0.02 ! Reference velocity (bulk velocity or wall velocity) real, parameter :: refVel = gradP/(3.0*vis) ! Gravitational acceleration real, dimension(3), parameter :: gr=(/0.0,0.0,0.0/) ! Output frequency integer,parameter :: iout0d = 100000, iout1d = 100000, iout2d = 10000000, iout3d = 10000000, ioutfld = 10000000 ! Power-law index real, parameter :: nn_n = 1.75 !THICK: 1.75 - THIN: 0.75 ! Fluid consistency index real, parameter :: nn_k=vis*(3.0*refVel/lz)**(1.0-nn_n)
main.f90
! Simulation initial step iStart = 0 ! Simulation final step iEnd = 1000000 ! Choose the timestep dt = 0.0002
Oldroyd-B fluid
We consider an Oldroyd-B fluid [1] with relaxation time λ=10 and polymeric viscossity μp=μ/4.
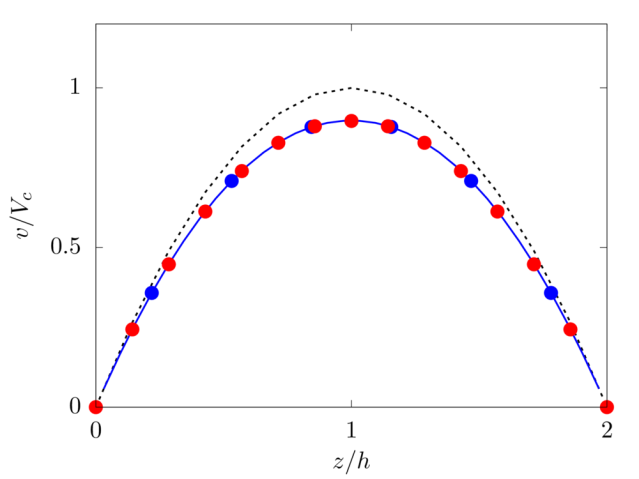
Analytical solution: v(z)=2Pyh2/(μ+μp)(z/2h)[1−(z/2h)].
config.h
#define _FLOW_CHANNEL_ #define _FLOW_CHANNEL_CPG_ #define _FLOW_CHANNEL_LAMINAR_ #define _SOLVER_FFT2D_ #define _MULTIPHASE_ #define _MULTIPHASE_NNF_ #define _MULTIPHASE_VISCOSITY_UNIFORM_ #define _MULTIPHASE_DENSITY_UNIFORM_ #define _MULTIPHASE_NNF_OLB_
param.f90
! Total number of grid points in X, Y and Z integer, parameter :: nxt = 4, nyt = 4, nzt = 32 ! Size of the domain in X, Y and Z real, parameter :: lx = 0.25, ly = 0.25, lz = 2.0 ! Fluid viscosity and density real, parameter :: vis = 0.01, rho = 1.0 ! Imposed pressure gradient real, parameter :: gradP = 0.02 ! Reference velocity (bulk velocity or wall velocity) real, parameter :: refVel = gradP/(3.0*vis) ! Gravitational acceleration real, dimension(3), parameter :: gr=(/0.0,0.0,0.0/) ! Output frequency integer,parameter :: iout0d = 100000, iout1d = 100000, iout2d = 10000000, iout3d = 10000000, ioutfld = 10000000 ! Polymeric viscosity and relaxation time real, parameter :: nnVis=vis/4.0, nnLambda=10.0
main.f90
! Simulation initial step iStart = 0 ! Simulation final step iEnd = 2000000 ! Choose the timestep dt = 0.0002
FENE-P fluid
We consider a FENE-P fluid [2] with relaxation time λ=10, polymeric viscosity μp=μ/4 and maximum dumbbell extension L=6.
Analytical solution [3]: u=2Pyh2/μ(z/2h)[1−(z/2h)]+3/(8Cμ)(A1/3+B−−C1/3+D−+A1/3−B+−C1/3−D+),
where
A±=Bh±√B2h2+A3,
B±=3Bh±√B2h2+A3,
C±=B(z−1)±√B2(z−1)2+A3,
D±=3B(z−1)±√B2(z−1)2+A3,
with
config.h
#define _FLOW_CHANNEL_ #define _FLOW_CHANNEL_CPG_ #define _FLOW_CHANNEL_LAMINAR_ #define _SOLVER_FFT2D_ #define _MULTIPHASE_ #define _MULTIPHASE_NNF_ #define _MULTIPHASE_VISCOSITY_UNIFORM_ #define _MULTIPHASE_DENSITY_UNIFORM_ #define _MULTIPHASE_NNF_FEN_
param.f90
! Total number of grid points in X, Y and Z integer, parameter :: nxt = 4, nyt = 4, nzt = 32 ! Size of the domain in X, Y and Z real, parameter :: lx = 0.25, ly = 0.25, lz = 2.0 ! Fluid viscosity and density real, parameter :: vis = 0.01, rho = 1.0 ! Imposed pressure gradient real, parameter :: gradP = 0.02 ! Reference velocity (bulk velocity or wall velocity) real, parameter :: refVel = gradP/(3.0*vis) ! Gravitational acceleration real, dimension(3), parameter :: gr=(/0.0,0.0,0.0/) ! Output frequency integer,parameter :: iout0d = 100000, iout1d = 100000, iout2d = 10000000, iout3d = 10000000, ioutfld = 10000000 ! Polymeric viscosity and relaxation time real, parameter :: nnVis=vis/4.0, nnLambda=10.0 ! FENE-P dumbbell extensibility real, parameter :: nnL2=6.0**2
main.f90
! Simulation initial step iStart = 0 ! Simulation final step iEnd = 2000000 ! Choose the timestep dt = 0.0002
Elastoviscoplatic fluid
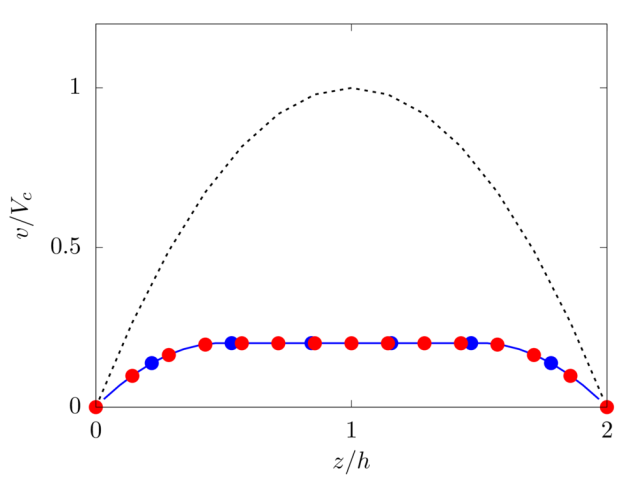
We consider an elastoviscoplastic fluid modelled with the Saramito model [4]. We fix the relaxation time λ=0.01, polymeric viscosity μp=μ/4 and yield stress τ0=0.01. Due to the low value of λ considered, we compare the result with the purely viscoplastic solution.
Analytical solution: v(z)=Py/2(μ+μp)[(z−1)2−h2]+τ0/(μ+μp)[(z−1)−h] if z0≤z−1<h else v(z)=v(z0+1).
config.h
#define _FLOW_CHANNEL_ #define _FLOW_CHANNEL_CPG_ #define _FLOW_CHANNEL_LAMINAR_ #define _SOLVER_FFT2D_ #define _MULTIPHASE_ #define _MULTIPHASE_NNF_ #define _MULTIPHASE_VISCOSITY_UNIFORM_ #define _MULTIPHASE_DENSITY_UNIFORM_ #define _MULTIPHASE_NNF_EVP_
param.f90
! Total number of grid points in X, Y and Z integer, parameter :: nxt = 4, nyt = 4, nzt = 32 ! Size of the domain in X, Y and Z real, parameter :: lx = 0.25, ly = 0.25, lz = 2.0 ! Fluid viscosity and density real, parameter :: vis = 0.01, rho = 1.0 ! Imposed pressure gradient real, parameter :: gradP = 0.02 ! Reference velocity (bulk velocity or wall velocity) real, parameter :: refVel = gradP/(3.0*vis) ! Gravitational acceleration real, dimension(3), parameter :: gr=(/0.0,0.0,0.0/) ! Output frequency integer,parameter :: iout0d = 100000, iout1d = 100000, iout2d = 10000000, iout3d = 10000000, ioutfld = 10000000 ! Polymeric viscosity and relaxation time real, parameter :: nnVis=vis/4.0, nnLambda=10.0/1000.0 ! Yield stress (tautau0 fluid-like behaviour) real, parameter :: nnTau0=0.01
main.f90
! Simulation initial step iStart = 0 ! Simulation final step iEnd = 2000000 ! Choose the timestep dt = 0.0002
Steady and periodic shear flow with EVP fluid
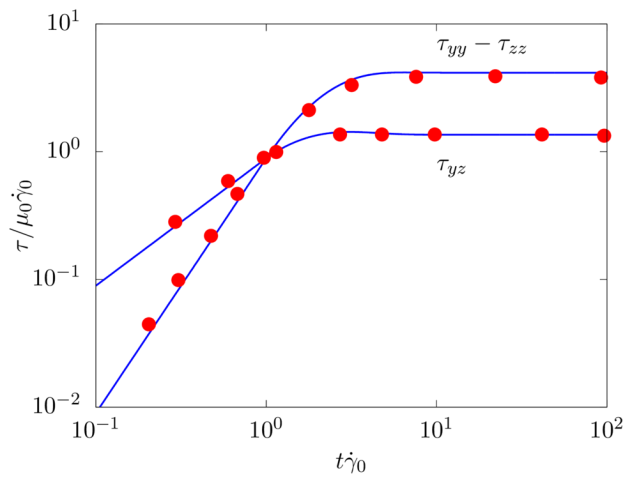
First, we consider a simple constant shear flow, with the shear rate ˙γ0: the Weissenberg number is fixed to Wi=λ˙γ0=1, the Bingham number Bi=τ0/[(μ+μp)˙γ0]=1, and the viscosity ratio β=μ/(μ+μp)=1/9.
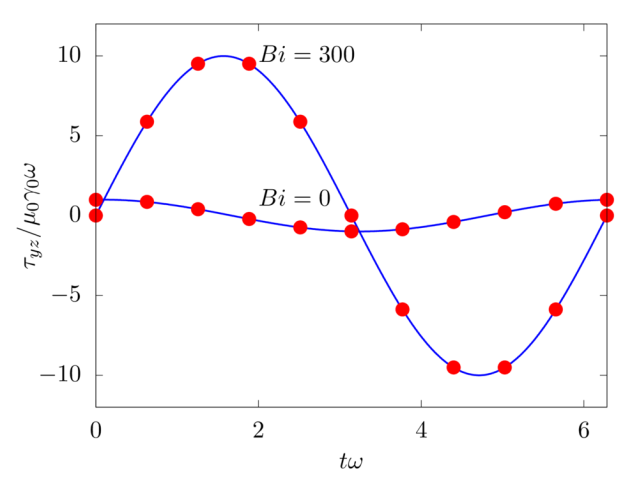
Next, we consider a time-periodic uniform shear flow, i.e. γ0sin(ω0t), where γ0 is the strain amplitude and ω0 the angular frequency of the oscillations. The Weissenberg number is Wi=λω0=0.1 and two Bingham numbers Bi=τ0/[(μ+μp)γ0ω0] are considered: Bi=0 and 300. Note that, when Bi=0, the material behaves like a viscoelastic fluid, and when Bi=300 as an elastic solid. The viscosity ratio β=μ/(μ+μp) is null in both cases, i.e. μ=0.
config.h
#define _FLOW_CHANNEL_ #define _FLOW_FIXED_ #define _SOLVER_FFT2D_ #define _MULTIPHASE_ #define _MULTIPHASE_NNF_ #define _MULTIPHASE_VISCOSITY_UNIFORM_ #define _MULTIPHASE_DENSITY_UNIFORM_ #define _MULTIPHASE_NNF_EVP_
param.f90
! Total number of grid points in X, Y and Z integer, parameter :: nxt = 4, nyt = 64, nzt = 64 ! Size of the domain in X, Y and Z real, parameter :: lx = 1.0, ly = 1.0, lz = 1.0 ! Fluid viscosity and density real, parameter :: vis = 0.0, rho = 1.0 !Steady: 1.0/9.0, 1.0 - Oscillating: 0.0, 1.0 ! Reference velocity (bulk velocity or wall velocity) real, parameter :: refVel = 0.5 ! Gravitational acceleration real, dimension(3), parameter :: gr=(/0.0,0.0,0.0/) ! Output frequency integer,parameter :: iout0d = 10, iout1d = 10000000, iout2d = 10000000, iout3d = 10000000, ioutfld = 10000000 ! Polymeric viscosity and relaxation time real, parameter :: nnVis=1.0, nnLambda=0.1 !Steady: 8.0/9.0, 1.0 - Oscillating: 1.0, 0.1 ! Yield stress (tautau0 fluid-like behaviour) real, parameter :: nnTau0=300.0 !Steady: 1.0 - Oscillating: 0.0/300.0
main.f90
! Simulation initial step iStart = 0 ! Simulation final step iEnd = 1000000 ! Choose the timestep dt = 0.001
References:
[1] J. G. Oldroyd. On the formulation of rheological equations of state. In Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, volume 200, pages 523–541. The Royal Society, 1950.
[2] A. Peterlin. Hydrodynamics of macromolecules in a velocity field with longitudinal gradient. Journal of Polymer Science: Polymer Letters, 4(4):287–291, 1966.
[3] D. O. A. Cruz, F. Pinho, and P. J. Oliveira. Analytical solutions for fully developed laminar flow of some viscoelastic liquids with a newtonian solvent contribution. Journal of Non-Newtonian Fluid Mechanics, 132(1-3):28–35, 2005.
[4] P. Saramito. A new constitutive equation for elastoviscoplastic fluid flows. Journal of Non-Newtonian Fluid Mechanics, 145(1):1–14, 2007.
Non-Newtonian multiphase flow
Rotation of a spherical particle in a Non-Newtonian Couette flow
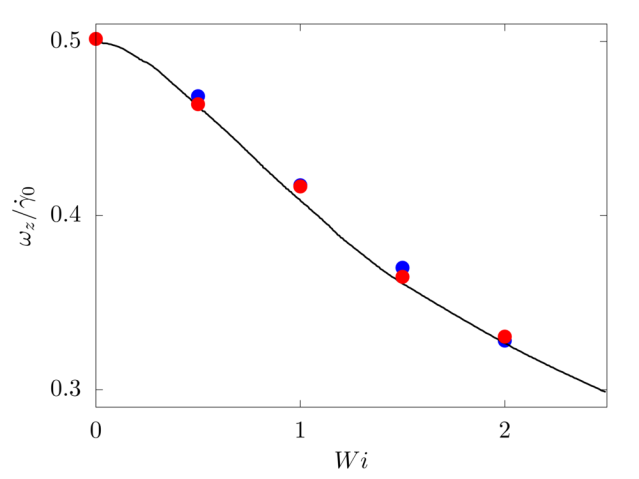
We consider a spherical particle of radius R immersed in a Non-Newtonian elastic fluid. The computational domain has size 4R×8R×8R and is discretised with 24 grid points per particle diameter. The top and bottom walls move with opposite velocity ±Vw, providing a shear rate ˙γ=2Vw/8R, while periodic boundary conditions are imposed in the remaining directions. The particle is neutrally buoyant, and the Reynolds number Re=ρ˙γR2/μ is fixed equal to 0.025. The fluid is modelled with the Oldroyd-B model and the Weissenberg number Wi=λ˙γ is varied between 0 and 2.
config.h
#define _FLOW_COUETTE_ #define _SOLVER_FFT2D_ #define _MULTIPHASE_ #define _MULTIPHASE_NNF_ #define _MULTIPHASE_IBM_ #define _MULTIPHASE_VISCOSITY_UNIFORM_ #define _MULTIPHASE_DENSITY_UNIFORM_ #define _MULTIPHASE_NNF_OLB_ #define _MULTIPHASE_NNF_XXX_LOG_ #define _MULTIPHASE_IBM_3D_
param.f90
!Total number of grid points in X, Y and Z integer, parameter :: nxt = 24*2, nyt = 24*4, nzt = 24*4 !Size of the domain in X, Y and Z real, parameter :: lx = 2.0, ly = 4.0, lz = 4.0 !Fluid viscosity and density real, parameter :: vis = 5.0, rho = 1.0 !Reference velocity (bulk velocity or wall velocity) real, parameter :: refVel = 1.0 !Gravitational acceleration real, dimension(3), parameter :: gr=(/0.0,0.0,-0.0/) !Output frequency integer,parameter :: iout0d = 500, iout1d = 1000000, iout2d = 1000000, iout3d = 1000000, ioutfld = 1000000 real, parameter :: nnVis=vis, nnLambda=4.0 integer, parameter :: ibmN=1 real, parameter :: ibmR = 0.5, ibmRho = rho, ibmRhoF = rho
main.f90
!Simulation initial step iStart = 0 !Simulation final step iEnd = 9999999 !Choose the timestep dt = 0.000001*32./24.
initPositionParticle.dat
1.0 2.0 2.0 0.5
References:
[1] F. Snijkers, G. D’Avino, P. L. Maffettone, F. Greco, M. A. Hulsen, and J. Vermant. Effect of vis- coelasticity on the rotation of a sphere in shear flow. Journal of Non-Newtonian Fluid Mechanics, 166(7-8):363–372, 2011.
[2] N. Goyal and J. J. Derksen. Direct simulations of spherical particles sedimenting in viscoelastic fluids. Journal of Non-Newtonian Fluid Mechanics, 183:1–13, 2012.